证明:( +1)(
+1)(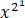 +1)⋯(
+1)⋯( +1)=(
+1)=(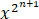 -1)/(x-1)
-1)/(x-1)
[n(1-1/3)(1-1/4)(1-1/5)…(1-1/(n+1))]的值等于【 】
设{an}是等差数列, a1=1,Sn是它的前n项和;{bn}是等比数列,其公比的绝对值小于1, Tn 是它的前n项和.如果a3=b2,S5=2T2-6,Tn =9,求{an },{bn}的通项公式.
已知等差数列{an}的公差d≠0,且a1,a3,a9成等比数列,则(a1+a3+a9)/(a2+a4+a10 )的值是________.
在各项均为正数的等比数列{an}中,若a5a6 = 9,则log3a1 + log3a2 + ... + log3a10 =【 】
等差数列{an},{bn}的前n项和分别为Sn与Tn,若Sn/Tn =2n/(3n+1),则an/bn 等于【 】
等比数列{an}的首项a1=-1,前n项和为Sn,若S10/S5 =31/32,则Sn 等于【 】
已知数列{an },{bn }都是由正数组成的等比数列,公比分别为p,q,其中p>q且p≠1,q≠1,设cn= an+bn,Sn为数列{cn}的前n项和.求Sn/Sn-1 .
给定整数n≥2,设M0 (x0,y0)是抛物线y2=nx-1与直线y=x的一个交点.试证明对任意正整数m,必存在整数k≥2,使(x0m,y0m)为抛物线y2=kx-1与直线y=x的一个交点.
设f(x)=x2+a,记f1(x)=f(x),fn(x)=f(fn-1(x)),n=2,3,⋯,M={a∈R│对所有正整数n,|fn(0)|≤2}.证明:M=[-2,1/4].
用数学归纳法证明下列恒等式 1³+2³+3³+⋯+n³=[n(n+1)/2]²
用数学归纳法求下列级数1/(1×2)+1/(2×3 )+1/(3×4)+⋯至n项之和.

