高中数学-高考试题(全国统考 1996年数列极限)

试题（1996年全国统考）

等比数列{a_n}的首项a₁=-1，前n项和为S_n，若S₁₀/S₅ =31/32,则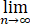S_n 等于【】

A、2/3

B、- 2/3

C、2

D、- 2

答案解析

B

讨论

数列极限

丘成桐女子赛数列极限

全国统考数列极限

求极限⁡[1/(n2+1)+2/(n2+1)+3/(n2+1)+⋯2n/(n2+1)].

已知等比数列{an}的公比q>1，并且a1=b(b≠0)，求⁡(a1+a2+a3+⋯+an)/(a6+a7+a8+⋯+an ).

已知{an}是等比数列，如果a1+a2+a3=18,a2+a3+a4=-9，且Sn=a1+a2+⋯+an，那么Sn 的值等于【】

已知{an}是公差不为零的等差数列，如果Sn是{an}的前n项和，那么⁡(nan)/Sn )等于______.

[n(1-1/3)(1-1/4)(1-1/5)…(1-1/(n+1))]的值等于【】

湖南省数列极限

等差数列{an},{bn}的前n项和分别为Sn与Tn，若Sn/Tn =2n/(3n+1)，则⁡an/bn 等于【】

极限(C22+C32+C42+⋯+Cn2)/(n(C21+C31+C41+⋯+Cn1))=【】

等比数列

已知 {an} 是无穷数列. 给出两个性质:① 对于 {an} 中任意两项 ai, aj (i > j), 在 {an} 中都存在一项 am, 使得 =am;② 对于 {an} 中任意一项 an (n ⩾ 3), 在 {an} 中都存在两项 ak, al (k > l), 使得 an = .(I) 若 an = n (n = 1, 2, …), 判断数列 {an} 是否满足性质 ①, 说明理由;(II) 若 an = 2n−1 (n = 1, 2, · · · ), 判断数列 {an} 是否同时满足性质 ① 和性质 ②, 说明理由;(III) 若 {an} 是递增数列, 且同时满足性质 ① 和性质 ②, 证明: {an} 为等比数列.

已知数列{an}的首项a1=b(b≠0)，它的前n项的和Sn=a1+a2+⋯+an (n≥1)，并且S1,S2,⋯,Sn,⋯是一个等比数列，其公比为p(p≠0，且|p|<1).(Ⅰ) 证明：a2,a3,⋯,an,⋯（即{an}从第2项起）是一个等比数列.(Ⅱ) 设Wn=a1 S1+a2 S2+⋯+an Sn (n≥1)，求Wn（用b,p表示）.

已知数列{an}的前n项和为Sn,且Sn=n-5an-85，n∈N*.（Ⅰ）证明：{an - 1} 是等比数列；（Ⅱ）求数列{Sn}的通项公式。请指出n为何值时，Sn取得最小值，并说明理由.

已知 {an} 是等比数列，且an > 0，a2a4 + 2a3a5 + a4a6 = 25，那么a3 + a5的值等于【】

设{an}是等差数列, a1=1,Sn是它的前n项和；{bn}是等比数列,其公比的绝对值小于1, Tn 是它的前n项和.如果a3=b2,S5=2T2-6,Tn =9,求{an },{bn}的通项公式.

在等差数列{an}中,若a10=0,则有等式a1+a2+⋯+an=a1+a2+⋯+a19-n (n<19,n∈N)成立.类比上述性质,相应地:在等比数列{bn}中,若b9=1,则有等式____________成立.

已知等比数列{an}的前3项和为168，a2-a5=42，则a6=【】

记Sn为等比数列{an}的前n项和，若S4=-5,S6=21S2，则S8=【】

我国度量衡的发展有着悠久的历史，战国时期就已经出现了类似于砝码的、用来测量物林质量的“环权”，已知9枚环权的质量(单位：铢)从小到大构成项数为9的数列{an}，该数列的前3项成等差数列,后7项成等比数列,且a1=1,a5=12,a9=192,则a7=______；数列{an}所有项的和为________.

已知等差数列{an}的公差d≠0,且a1,a3,a9成等比数列,则(a1+a3+a9)/(a2+a4+a10 )的值是________.

数列

信息熵是信息论中的一个重要概念. 设随机变量 X 所有可能的取值为 1, 2, … , n, 且 P (X = i) = pi >0 (i = 1, 2, …, n), =1, 定义 X 的信息熵 H(X) = −log2 pi.【】

将数列 {2n − 1} 与 {3n − 2} 的公共项从小到大排列得到数列 {an}, 则 {an} 的前 n 项和为 __________.

已知 {an} 为等差数列, {bn} 为等比数列, a1 = b1 = 1, a5 = 5(a4 − a3), b5 = 4(b4 − b3).(I) 求 {an} 和 {bn} 的通项公式;(II) 记 {an} 的前 n 项和为 Sn, 求证: SnSn+2 < Sn+12 (n ∈ N∗);(III) 对任意的正整数 n, 设 cn = .求数列 {cn} 的前 2n 项和.

已知有限数列 {an} 项数为 m, 若其满足: |a1 − a2| ⩽ |a1 − a3| ⩽ · · · ⩽ |a1 − am|, 则称数列 {an} 满足性质 P .(1) 判断数列 3, 2, 5, 1 和数列 4, 3, 2, 5, 1 是否具有性质 P ;(2) 已知 a1 = 1, 公比为 q 的等比数列, 项数为 10, 具有性质 P , 求 q 的取值范围;(3) 若 an 是 1, 2, 3, · · · , m (m ⩾ 4) 的一个排列, bk = ak+1 (k = 1, 2, 3 · · · , m − 1), 数列 {an}, {bn} 都具有性质 P , 求所有满足条件的 {an}.

已知数列 {an}, {bn}, {cn} 中, a1 = b1 = c1 = 1, cn+1 = an+1 − an, cn+1=bn/bn+2 ∙cn (n ∈ N∗).(I) 若数列 {bn} 为等比数列, 且公比 q > 0, 且 b1 + b2 = 6b3, 求 q 的值及数列 {an} 的通项公式;(II) 若数列 {bn} 为等差数列, 且公差 d > 0, 证明: c1 + c2 + … + cn < 1 +1/d , n ∈ N∗.

试问数列：lg100,lg⁡(100sinπ/4),lg⁡(100sin2π/4),⋯,lg⁡(100sinn-1π/4)，前多少项的和的值最大？并求出这大值（这里取lg2=0.301）

已知以AB为直径的半圆有一个内接正方形CDEF，其边长为1（如图）.设AC=a,BC=b,作数列u1=a-b,u2=a2-ab+b2,u3=a3-a2b+ab2-b3,...uk=ak-ak-1b+ak-2b2-...+(-1)kbk;求证：un=un-1+un-2 (n≥3).

已知数列a1,a2,⋯an,⋯和数列b1,b2,⋯bn,⋯，其中a1=p,b1=q,an=pan-1,bn=qan-1+rbn-1 (n≥2)（p,q,r是已知常数，且q≠0,p>r>0）.(1) 用p,q,r,n表示bn，并用数学归纳法加以证明；(2) 求.

全国统考数列与推理

已知x1>0,x≠1,且xn+1=,(n=1,2,⋯).试证：数列{xn}或者对任意自然数n都满足xn<xn+1，或者对任意自然数n都满足xn>xn+1.