已知 {an} 是无穷数列. 给出两个性质:
① 对于 {an} 中任意两项 ai, aj (i > j), 在 {an} 中都存在一项 am, 使得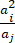 =am;
=am;
② 对于 {an} 中任意一项 an (n ⩾ 3), 在 {an} 中都存在两项 ak, al (k > l), 使得 an = 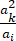 .
.
(I) 若 an = n (n = 1, 2, …), 判断数列 {an} 是否满足性质 ①, 说明理由;
(II) 若 an = 2n−1 (n = 1, 2, · · · ), 判断数列 {an} 是否同时满足性质 ① 和性质 ②, 说明理由;
(III) 若 {an} 是递增数列, 且同时满足性质 ① 和性质 ②, 证明: {an} 为等比数列.
(I) 若 an = n (n = 1, 2, … ), { an } 不满足性质 ①: a3 = 3, a2 = 2, 则 =9/2 ∉ N*.(II) 若 an = 2n−1 (n = 1, 2, · · · ), 数列 {an} 同时满足性质 ① 和性质 ②对 {an} 中任意两项 ai, aj (i > j), = = = a2i−j = am, 即存在 m = 2i − j 满足性质 ①.对 {an} 中任意一项 an (n ⩾ 3), an = 2n−1 = 22(k−l)−1 = , 即存在 k, l, 使得 n = 2k − l 成立即可, 满足性质 ②.(III) 假设 k ⩽ n 时, 有 ak = a1qk−1, 对 an+1 由性质 ②, ∃ 正整数 i > j, 使 an+1 = .又 {an} 递增, 所以 ai > aj.若 a1 > 0, 则 ai > aj > 0 ⇒ an+1 = > ai × 1 = ai > aj, 所以 j < i < n + 1, 所以ai = a1qi−1, aj = a1qj−1,an+1 = = a1q2(i-1...
查看完整答案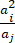 =am;
=am;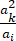 .
.
