• 关注优题吧，注册平台账号.

题吧，智能辅助学习中心
  2. 高中数学
  3. 数列
  4. 等比数列
  2. 知识库
  3. 试卷库

单项选择（2022年全国乙·理）

已知等比数列{an}的前3项和为168，a2-a5=42，则a6=【 】

A、14

B、12

C、6

D、3

答案解析

D

【解析】

设等比数列{an}的公比为q,q≠0，

若q=1，则a2-a5=0，与题意矛盾，

所以q≠1，

则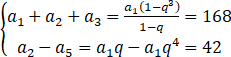，解得，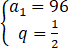

所以a6=a1q5=3.

讨论

高中数学

在正方体ABCD-A1B1C1D1中，E，F分别为AB,BC的中点，则【 】

执行下面的流程图，输出的n=【 】

设F为抛物线C:y2=4x的焦点，点A在C上，点B(3,0)，若|AF|=|BF|，则|AB|=【 】

已知向量a,b满足|a|=1,|b|=√3,|a-2b|=3，则a⋅b=【 】

嫦娥二号卫星在完成探月任务后，继续进行深空探测，成为我国第一颗环绕太阳飞行的人造行星，为研究嫦娥二号绕日周期与地球绕日周期的比值，用到数列{bn}：b1=1+ ，b2=1+，b3=1+，…，依此类推，其中αk∈N* (k=1,2,⋯)．则【 】

已知z=1-2i，且z+az ̄+b=0，其中a，b为实数，则【 】

设全集U={1,2,3,4,5}，集合M满足∁UM={1,3}，则【 】

设抛物线C:y2=2px(p>0)的焦点为F，点D(p,0)，过F的直线交C于M，N两点．当直线MD垂直于x轴时，|MF|=3．（1）求C的方程；（2）设直线MD,ND与C的另一个交点分别为A，B，记直线MN,AB的倾斜角分别为α,β．当α-β取得最大值时，求直线AB的方程．

已知函数f(x)=x3-x,g(x)=x2+a，曲线y=f(x)在点(x1,f(x1))处的切线也是曲线y=g(x)的切线．（1）若x1=-1，求a；（2）求a的取值范围．

小明同学参加综合实践活动，设计了一个封闭的包装盒，包装盒如图所示：底面ABCD是边长为8（单位：cm）的正方形，△EAB,△FBC,△GCD,△HDA均为正三角形，且它们所在的平面都与平面ABCD垂直． （1）证明：EF//平面ABCD；（2）求该包装盒的容积（不计包装盒材料的厚度）．

等比数列

设{an}是由正数组成的等比数列，Sn是其前n项和.(1)证明(lgSn+lgSn+2)/2<lgSn+1.(2)是否存在常数c>0，使得[lg(Sn-c)+lg⁡(Sn+2-c)]/2=lg(Sn+1-c)成立？并证明你的结论.

如图为一台冷轧机的示意图.冷轧机由若干对轧辊组成,带钢从一端输入,经过各对轧辊逐步减薄后输出. (I)输入带钢的厚度为α,输出带钢的厚度为β,若每对轧辊的减薄率不超过r0.问冷轧机至少需要安装多少对轧辊?[一对轧辊减薄率= (输入该对的带钢厚度-从该对输出的带钢厚度) ÷输入该对的带钢厚度](Ⅱ)已知一台冷轧机共有4对减薄率为20%的轧辊，所有轧辊周长均为1600 mm.若第k对轧辊有缺陷，每滚动一周在带钢上压出一个疵点,,在冷轧机输出的带钢上,疵点的间距为Lk.为了便于检修,请计算L1 、L2 、L3并填入下表(轧钢过程中,带钢宽度不变，且不考虑损耗).

已知数列{cn},其中cn=2n+3n,且数列{cn+1 - pcn}为等比数列，求常数p.

设{cn}，{bn}是公比不相等的两个比数列，cn =an+bn.证明数列{cn}不是等比数列.

在等差数列{an}中,若a10=0,则有等式a1+a2+⋯+an=a1+a2+⋯+a19-n (n<19,n∈N)成立.类比上述性质,相应地:在等比数列{bn}中,若b9=1,则有等式____________成立.

设{an}是公比为q的等比数列，Sn是它的前n项和.若{Sn}是等差数列，则q=________.

设数列{an}是公比q>0的等比数列，Sn是它的前n项和，若Sn=7，则此数列的首项a1的取值范围是________.

记Sn为等比数列{an}的前n项和，若S2=4,S4=6，则S6=【 】

已知{an}为无穷等比数列，a1=3,an的各项和为9，bn=a2n，则数列{bn}的各项和为__________.

已知a,a∈R,ab>0，函数f(x)=ax2+bx(x∈R).若f(s-t),f(s),f(s+t)成等比数列，则平面上点(s,t)的轨迹是【 】

数列

已知数列a1,a2,⋯an,⋯和数列b1,b2,⋯bn,⋯，其中a1=p,b1=q,an=pan-1,bn=qan-1+rbn-1 (n≥2)（p,q,r是已知常数，且q≠0,p>r>0）.(1) 用p,q,r,n表示bn，并用数学归纳法加以证明；(2) 求.

全国统考数列与推理

求极限⁡[1/(n2+1)+2/(n2+1)+3/(n2+1)+⋯2n/(n2+1)].

已知等比数列{an}的公比q>1，并且a1=b(b≠0)，求⁡(a1+a2+a3+⋯+an)/(a6+a7+a8+⋯+an ).

已知{an}是等比数列，如果a1+a2+a3=18,a2+a3+a4=-9，且Sn=a1+a2+⋯+an，那么Sn 的值等于【 】

已知{an}是公差不为零的等差数列，如果Sn是{an}的前n项和，那么⁡(nan)/Sn )等于______.

[n(1-1/3)(1-1/4)(1-1/5)…(1-1/(n+1))]的值等于【 】

湖南省数列极限

等差数列{an},{bn}的前n项和分别为Sn与Tn，若Sn/Tn =2n/(3n+1)，则⁡an/bn 等于【 】

已知数列{an }，{bn }都是由正数组成的等比数列，公比分别为p,q，其中p>q且p≠1,q≠1，设cn= an+bn，Sn为数列{cn}的前n项和.求Sn/Sn-1 .