已知z=1-2i，且z+az ̄+b=0，其中a，b为实数，则【 】
A、a=1,b=-2
B、a=-1,b=2
C、a=1,b=2
D、a=-1,b=-2
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
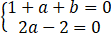,即
设全集U={1,2,3,4,5}，集合M满足∁UM={1,3}，则【 】
已知函数f(x)=x3-x,g(x)=x2+a，曲线y=f(x)在点(x1,f(x1))处的切线也是曲线y=g(x)的切线．（1）若x1=-1，求a；（2）求a的取值范围．
记双曲线C:x2/a2 -y2/b2 =1(a>0,b>0)的离心率为e，写出满足条件“直线y=2x与C无公共点”的e的一个值_________．
设点M在直线2x+y-1=0上，点(3,0)和(0,1)均在⊙M上，则⊙M的方程为______________．
已知向量a=(m,3),b=(1,m+1)．若a⊥b，则m=__________．
已知椭圆C:x2/a2 +y2/b2 =1(a>b>0)的离心率为1/3，A1,A2分别为C的左、右顶点，B为C的上顶点．若(BA1)⋅(BA2)=-1，则C的方程为【 】
设p≠0，实系数一元二次方程z2-2pz+q=0有两个虚数根z1,z2.再设z1,z2在复平面内的对应点是Z1,Z2.求以Z1,Z2为焦点且经过原点的椭圆的长轴的长.
在复平面内，若复数z满足|z+1|=|z-i|，则z所对应的点Z的集合构成的图形是【 】
复平面上点A,B对应的复数分别为z1=2,z2=-3，点P对应的复数为z,(z-z1)/(z-z2 )的辐角主值为φ.当点P在以原点为圆心，1为半径的上半圆周（不包括两个端点）上运动时，求φ的最小值.
已知z1,z2是两个给定的复数，且z1≠z2，它们在复平面上分别对应于点Z1和点Z2.如果z满足方程|z-z1|-|z-z2|=0,那么z对应的点Z的集合是【 】
在复平面上，一个正方形的四个顶点按照逆时针方向依次为Z1,Z2,Z3,O(其中O为原点)，已知Z2对应复数z2=1+i，求Z1和Z3对应的复数.
已知复数z=/2 - 1/2 i,ω=/2+/2 i.复数,z2ω3在复数平面上所对应的点分别为P,Q.证明△OPQ是在等腰直角三角形（其中O为原点）.