设O为复平面的原点,Z1和Z2为复平面内的两个动点,且满足:
(Ⅰ) Z1和Z1所对应的复数的辐角分别为定值θ和-θ (0<θ<π/2);
(Ⅱ) △OZ1 Z2的面积为定值S.
求△OZ1 Z2的重心Z所对应的复数的模的最小值.
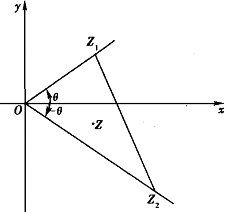
设O为复平面的原点,Z1和Z2为复平面内的两个动点,且满足:
(Ⅰ) Z1和Z1所对应的复数的辐角分别为定值θ和-θ (0<θ<π/2);
(Ⅱ) △OZ1 Z2的面积为定值S.
求△OZ1 Z2的重心Z所对应的复数的模的最小值.

设Z1,Z2和Z对应的复数分别为z1,z2和z,其中z1=r1 (cosθ+isinθ),z2=r2 (cosθ-isinθ).由于Z是△OZ1 Z2的重心,根据复数加法的几何意义,有3z=z1+z2=(r1+r2)cosθ+(r1-r2)isinθ.于是|3z|2=(r1+r2)2 cos2 θ+(r1-r2)2 sin2 θ =(r1-r2)2 cos2 θ+4r1 r2 cos2 ...
查看完整答案设p≠0,实系数一元二次方程z2-2pz+q=0有两个虚数根z1,z2.再设z1,z2在复平面内的对应点是Z1,Z2.求以Z1,Z2为焦点且经过原点的椭圆的长轴的长.
在复平面上,一个正方形的四个顶点按照逆时针方向依次为Z1,Z2,Z3,O(其中O为原点),已知Z2对应复数z2=1+i,求Z1和Z3对应的复数.
已知z1,z2是两个给定的复数,且z1≠z2,它们在复平面上分别对应于点Z1和点Z2.如果z满足方程|z-z1|-|z-z2|=0,那么z对应的点Z的集合是【 】
在复平面内,若复数z满足|z+1|=|z-i|,则z所对应的点Z的集合构成的图形是【 】
复平面上点A,B对应的复数分别为z1=2,z2=-3,点P对应的复数为z,(z-z1)/(z-z2 )的辐角主值为φ.当点P在以原点为圆心,1为半径的上半圆周(不包括两个端点)上运动时,求φ的最小值.
已知a,b∈R,a+3i=(b+i)i(i为虚数单位),则【 】
已知复数z的辐角为60°,且|z-1|是|z|和|z-2|的等比中项求|z|.
设z是虚部不为零的复数.若(2+3z+4z2)/(2-3z+4z2)是实数,则|z|2的值为__________.
在复数范围内,方程z ̅-z2=i(z ̅+z2)的解的个数为__________.
设z是不为0的复数,若(z ̅ )2+1/z2 的实部和虚部均为整数,则|z|的值可能是【 】
求1的三次根(实根和虚根),证:任一虚根的平方等于另一虚根,且((-1+i√3)/2)n+((-1-i√3)/2)n=-1,式中n为整数,唯不能为3的倍数.