高中数学-高考试题(上海市 1990年复平面)

问答题（1990年上海市）

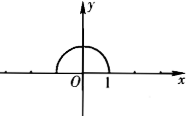
复平面上点A,B对应的复数分别为z₁=2,z₂=-3，点P对应的复数为z,(z-z₁)/(z-z₂ )的辐角主值为φ.当点P在以原点为圆心，1为半径的上半圆周（不包括两个端点）上运动时，求φ的最小值.

答案解析

设z=x+yi，则x2+y2=1,y>0,(z-z1)/(z-z2 )=(x-2+yi)/(x+3+yi) = + .令ω=u+iv=(z-z1)/(z-z2 )，则v=5y/((x+3)2+y2 )>0,且z=(3ω+2)/(1-ω)又|z|=1 ∴ |3ω+2|=|1-ω|，即|(3u+2)+...

查看完整答案

讨论

高中数学

如图，平面α,β相交于直线MN，点A在平面α上，点B在平面β上，点C在直线MN上，∠ACM=∠BCN=45°，A-MN-B是60°的二面角，AC=1. 求：(1) 点A到平面β的距离；(2) 二面角A-BC-M的大小（用反三角函数表示）.

关于实数x的不等式|x - (a+1)2/2| ≤ (a+1)2/2 与 x2 - 3(a+1)x + 2(3a+1)≤0(a∈R)的解集依次记为A和B，求使A⊆B的a的取值范围.

已知直线l:x - ny = 0(n∈N)；圆M:(x+1)2 + (y+1)2 = 1；抛物线Φ:y=(x-1)2.又l与M交于点A,B；l与Φ交于点C,D.求⁡|AB|2/|CD|2.

已知点P在直线x=2上移动，直线l通过原点且与OP垂直，通过点A(1,0)及点P的直线m和直线l交于点Q.求点Q的轨迹方程，并指出该迹的名称和它的焦点坐标.

求方程 + sinx = 0在[0,2π)上的解.

已知log5(x2+2x-2) = 0 , 2log5(x+2) - log5y + 1/2 = 0，求y的值.

下列四个函数中，在定义域内不具有单调性的函数是【】

设a,b是两条异面直线，那么下列四个命题中的假命题是【】

已知1<x<d，令a=(logdx)2,b=logd(x2),c=logd(logdx)，则【】

函数f(x)=atan(x/a)的最小正周期是【】

复平面

在复平面内，(1+3i)(3-i)对应的点位于【】

用数学归纳法证明等式对一切自然数n都成立.

设p≠0，实系数一元二次方程z2-2pz+q=0有两个虚数根z1,z2.再设z1,z2在复平面内的对应点是Z1,Z2.求以Z1,Z2为焦点且经过原点的椭圆的长轴的长.

设O为复平面的原点，Z1和Z2为复平面内的两个动点，且满足：(Ⅰ) Z1和Z1所对应的复数的辐角分别为定值θ和-θ (0<θ<π/2);(Ⅱ) △OZ1 Z2的面积为定值S.求△OZ1 Z2的重心Z所对应的复数的模的最小值.

在复平面内，若复数z满足|z+1|=|z-i|，则z所对应的点Z的集合构成的图形是【】

在复平面上，一个正方形的四个顶点按照逆时针方向依次为Z1,Z2,Z3,O(其中O为原点)，已知Z2对应复数z2=1+i，求Z1和Z3对应的复数.

已知复数z0=1-mi(m>0),z=x+yi和w=x'+y'i,其中x,y,x',y'均为实数, i为虚数单位,且对于任意复数z,有w=z ̅0∙ z ̅ ,|w|=2|z|.(I)试求m的值,并分别写出x'和y'用x,y表示的关系式.(Ⅱ)将(x,y)作为点P的坐标, (x',y')作为点Q的坐标,上述关系式可以看作是坐标平面上点的一个变换:它将平面上的点P变到这一平面上的点Q.当点P在直线y=x+1上移动时,试求点P经该变换后得到的点Q的轨迹方程.(Ⅲ)是否存在这样的直线:它上面的任一点经上述变换后得到的点仍在该直线上?若存在,试求出所有这些直线;若不存在,则说明理由.

已知z1,z2是两个给定的复数，且z1≠z2，它们在复平面上分别对应于点Z1和点Z2.如果z满足方程|z-z1|-|z-z2|=0,那么z对应的点Z的集合是【】

对任意函数f(x),x∈D，可按图示构造一个数列发生器，其工作原理如下：①输入数据x0∈D，经数列发生器输出x1=f(x0 )；②若x1∉D，则数列发生器结束工作；若x1∈D，将x1反馈回输入端，再输出x2=f(x1 )，并依此规律继续下去，现定义f(x)=(4x-2)/(x+1). （Ⅰ）若输入x0=49/65，则由数列发生器产生数列{xn }，请写出数列{xn }的所有项；（Ⅱ）若要数列发生器生产一个无穷的常数数列，试求输入的初始数据x0的值.（Ⅲ）若输入x0时，产生的无穷数列{xn }满足：对任意正整数n，均有xn<xn+1，求x0的取值范围.

2010年上海世博会园区每天9:00开园，20:00停止入园.在下面的框图中，S表示上海世博会官方网站在每个整点报道的入园总人数，a表示整点报道前1个小时内入园人数，则空白的执行框内应填入__________.

数系与复数

设复数z1和z2满足关系式=0，其中A为不等于0的复数.证明：(1)| z1+A||z2+A|=|A|2;(2) =||.

((1-i)/(1+i))2的值等于【】

设复数z满足关系式z+|z ̅|=2+i，那么z等于【】

设a≥0，在复数集C中解方程z2+2|z|=a.

设{zn } (n≥1)是复数数列，奇数项为实数，偶数项为纯虚数，且∀k∈N+,|zkzk+1| = 2k，记fn=|z1 + z2 + ⋯ + zn |.(1) 求f2020的最小可能值；(2) 求f2020∙f2021的最小可能值.

设复数ω = cos(2π/5) + isin(2π/5)，则ω + ω2 + ω3 + ω4 + ω5的值是________.

设i是虚数单位，复数(9+2i)/(2+i)=__________.

已知a∈R,(1+ai)i=3+i，(i为虚单位)，则a=【】

若i(i-z)=1，则z ̅+z=【】

(2+2i)(1-2i)=【】