小明同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图所示:底面ABCD是边长为8(单位:cm)的正方形,△EAB,△FBC,△GCD,△HDA均为正三角形,且它们所在的平面都与平面ABCD垂直.
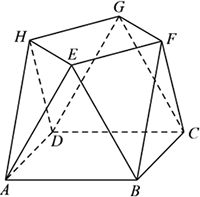
(1)证明:EF//平面ABCD;
(2)求该包装盒的容积(不计包装盒材料的厚度).
小明同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图所示:底面ABCD是边长为8(单位:cm)的正方形,△EAB,△FBC,△GCD,△HDA均为正三角形,且它们所在的平面都与平面ABCD垂直.

(1)证明:EF//平面ABCD;
(2)求该包装盒的容积(不计包装盒材料的厚度).
(1)分别取AB,BC的中点M,N,连接MN,因为△EAB,△FBC为全等的正三角形,所以EM⊥AB,FN⊥BC,EM=FN,又平面EAB⊥平面ABCD,平面EAB∩平面ABCD=AB,EM⊂平面EAB,所以EM⊥平面ABCD,同理可得FN⊥平面ABCD,根据线面垂直的性质定理可知EM//FN,而EM=FN,所以四边形EMNF为平行四边形,所以EF//MN,又EF⊄平面ABCD,MN⊂平面ABCD,所以EF//平面ABCD. (2)分别取AD,DC的中点K,L,由(1)知,EF//MN且EF=M...
查看完整答案向高为H的水瓶中注水,注满为止.如果注水量V与水深h的函数关系的图像如图所示,那么水瓶的形状是【 】
如图,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF//AB,EF=3/2,EF与面AC的距离为2,则该多面体的体积为【 】
设正多面体每个顶点连有M条棱,每面都是正N边形,则正整数M和N满足关系:M>2,N>2,MN<2(M+N),这种正多面体共有【 】种。
已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为________.
设集合M={1,3,5,7,9},N={x|2x>7},则M∩N=【 】
设集合A={-2,-1,0,1,2},B={x∣0≤x<5/2},则A∩B=【 】