高中数学-高考试题(全国统考 1988年数列极限)

计算题（1988年全国统考）

已知等比数列{a_n}的公比q>1，并且a₁=b(b≠0)，求⁡(a₁+a₂+a₃+⋯+a_n)/(a₆+a₇+a₈+⋯+a_n ).

答案解析

原式=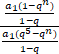=⁡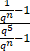=⁡=(0-1)/(0-1)=1.

讨论

高中数学

如图，四棱锥S-ABCD的底面是边长为1的正方形，侧棱SB垂直于底面，并且SB=，用α表示∠ASD，求sinα的值.

已知sinθ=-3/5,3π<θ<7π/2，求tanθ/2的值.

解方程9-x - 2∙31-x = 27.

求复数-i的模和辐角的主值.

如图，已知二面角α-AB-β的平面角是锐角，C是平面α内的一点（它不在棱AB上），点D是点C在平面β上的射影，点E是棱AB上满足∠CEB为锐角的任意一点，那么【】.

假设在200件产品中有3件是次品，现在从中任意抽取5件，其中至少有2件次品的抽法有【】种.

如果曲线x2-y2-2x-2y-1=0经过平移坐标轴后的新方程为x'2-y'2=1，那么新坐标系的原点在原坐标系中的坐标为【】

在复平面内，若复数z满足|z+1|=|z-i|，则z所对应的点Z的集合构成的图形是【】

设命题甲：△ABC的一个内角为60°. 命题乙：△ABC的三内角的度数成等差数列. 那么【】

tan(arctan1/5+arctan3)的值等于【】

数列极限

已知等差数列前三项为a,4,3a前n项的和为Sn，Sk=2550.(Ⅰ)求a及k的值,(Ⅱ)求 (1/S1 +1/S2 +⋯+1/Sn ).

已知数列{an }，{bn }都是由正数组成的等比数列，公比分别为p,q，其中p>q且p≠1,q≠1，设cn= an+bn，Sn为数列{cn}的前n项和.求Sn/Sn-1 .

在等比数列{an}中，a1>1，且前n项和Sn满足Sn=1/a1 ，那么a1的取值范围是【】

极限(C22+C32+C42+⋯+Cn2)/(n(C21+C31+C41+⋯+Cn1))=【】

丘成桐女子赛数列极限

全国统考数列极限

求极限⁡[1/(n2+1)+2/(n2+1)+3/(n2+1)+⋯2n/(n2+1)].

计算：(n/n+2)n=________.

等差数列{an},{bn}的前n项和分别为Sn与Tn，若Sn/Tn =2n/(3n+1)，则⁡an/bn 等于【】

等比数列{an}的首项a1=-1，前n项和为Sn，若S10/S5 =31/32,则Sn 等于【】

数列

已知{an}是公差为2的等差数列，其前8项的和为64，{bn}是公比大于0的等比数列，b1=4,b3-b2=48.(1)求{an}和{bn}的通项公式；(2)记cn=b2n+1/bn ,n∈N*(i)证明{cn2-c2n}是等比数列；(ii)证明<2√2.

嫦娥二号卫星在完成探月任务后，继续进行深空探测，成为我国第一颗环绕太阳飞行的人造行星，为研究嫦娥二号绕日周期与地球绕日周期的比值，用到数列{bn}：b1=1+ ，b2=1+，b3=1+，…，依此类推，其中αk∈N* (k=1,2,⋯)．则【】

己知数列{an}各项均为正数，其前n项和Sn满足an⋅Sn=9(n=1,2,⋯)．给出下列四个结论：①{an}的第2项小于3； ②{an}为等比数列；③{an}为递减数列； ④{an}中存在小于1/100的项．其中所有正确结论的序号是__________．

已知Q:a1,a2,⋯,ak为有穷整数数列．给定正整数m，若对任意的n∈{1,2,⋯,m}，在Q中存在ai,ai+1,ai+2,⋯,ai+j (j≥0)，使得ai+ai+1+ai+2+⋯+ai+j=n，则称Q为m-连续可表数列．（1）判断Q:2,1,4是否为5-连续可表数列？是否为6-连续可表数列？说明理由；（2）若Q:a1,a2,⋯,ak为8-连续可表数列，求证：k的最小值为4；（3）若Q:a1,a2,⋯,ak为20-连续可表数列，且a1+a2+⋯+ak<20，求证：k≥7．

已知数列{an}满足a1=1,an+1=an-1/3 an2 (n∈N* )，则【】

数列{an}中，a1=1,a2=3，若地任意n(n≥2)都存在正整数i(1≤i≤n-1)使得an+1=2an-ai.(1)求a4的所有可能值.(2)命题p：若a1,a2,a3,…,a8成等差数列，则a9<30，证明命题p为真；写出p的逆命题q，并判断q的真假，若命题q为真则证明，若命题q为假，请举出反例.(3)若对任意正整数m,a2m=3m，求数列{an}的通项公式.

数列{an },{bn}满足(3ak+5)=55,(ak+bk)=32，求bk 的值.

有相交之二直线 a 及 b，自 a 上之一点作 b 之垂线，复自其在 b 上之垂足向 a作垂线，更自第二个垂足作 b 之垂线，如此继续作成无数根垂线，设第一垂线之长为 7，第二垂线之长为 6，求此无数垂线长之和.

设a,b,c三数成调和级数，试证1/a+1/c+1/(a-b)+1/(c-b)=0.

问级数1-x/√1+x²/√2-x³/√3+⋯何时收敛？