已知{an}是公差为2的等差数列,其前8项的和为64,{bn}是公比大于0的等比数列,b1=4,b3-b2=48.
(1)求{an}和{bn}的通项公式;
(2)记cn=b2n+1/bn ,n∈N*
(i)证明{cn2-c2n}是等比数列;
(ii)证明
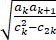 <2√2.
<2√2.
已知{an}是公差为2的等差数列,其前8项的和为64,{bn}是公比大于0的等比数列,b1=4,b3-b2=48.
(1)求{an}和{bn}的通项公式;
(2)记cn=b2n+1/bn ,n∈N*
(i)证明{cn2-c2n}是等比数列;
(ii)证明
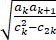 <2√2.
<2√2.
(1)设{an}的公差为d,前n项和为Sn,{bn}的公比为q(q>0).由题意得d=2,S8=8a1+(8×(8-1))/2×d=8a1+56=64,解得a1=1.∴an=a1+d(n-1)=1+2(n-1)=2n-1,n∈N*.根据题意,b1=4,b_3-b2=b1 q2-b1 q=4q2-4q=48,化简得q2-q-12=0,解得q=4或q=-3(舍去),∴bn=b1 qn-1=4n,n∈N*.∴{an}的通项公式为an=2n-1,n∈N*;{bn}的通项公式为bn=4n,n∈N*.(2)由(1)得cn=b2n+1/bn =42n+1/4n ,n∈N*,(i) cn2-c2n=(42n+1/4n )2-(44n+1/42n )=44n+2∙4n+1/42n -44n-1/42n =2∙4n,n∈N...
查看完整答案在等差数列 {an} 中, a1 = −9, a5 = −1. 记 Tn = a1a2 · · · an (n = 1, 2, · · · ), 则数列 {Tn}【 】
已知数列 {an} 为不为零的等差数列, 且 a1 + a10 = a9, 则 (a1+a2+⋯+a9)/a10 =__________ .
已知等差数列 {an} 的前 n 项和为 Sn, 公差 d≠ 0, a1/d ⩽ 1. 记 b1 = S2, bn+1 = Sn+2 − S2n, n ∈ N∗, 下列不可能成立的是【 】
我国古代数学家杨辉、宋世杰等研究过高阶等差数列求和问题, 如数列 {n(n+1)/2} 就是二阶等差数列,数列{n(n+1)/2} (n ∈ N∗) 的前 3 项和是________.
若(z-x)2-4(x-y)(y-z)=0,求证:x,y,z成等差数列.
设等差数列{an}的前n项和为Sn.已知a3=12,S12>0,S13<0.(Ⅰ)求公差d的取值范围.(Ⅱ)指出S1,S2,…,S12中哪一个值最大,并说明理由.
已知数列{an}满足a1=1,an+1=(1)记bn=a2n,写出b1,b2,并求数列{bn}的通项公式;(2)求{an}的前20项和.
数列{an}是递增的整数数列,且a1≥3,a1+a2+⋯+an=100,则n的最大值为【 】
已知ai∈N* (i=1,2,…,9)对任意的k∈N* (2≤k≤8),ak=ak-1+1或ak=ak+1-1中有且仅有一个成立,a1=6,a9=9,则a1+⋯+a9的最小值为__________.
数列 {an} 满足 an+2 + (−1)nan = 3n − 1, 前 16 项和为 540, 则 a1 = ______.
数列 {an} 中, a1 = 2, am+n = aman , 若 ak+1 + ak+2 + · · · + ak+10 = 215 − 25, 则 k=【 】
设数列 {an} 满足 a1 = 3, an+1 = 3an − 4n.(1) 计算 a2, a3, 猜想 {an} 的通项公式并加以证明;(2) 求数列 {2nan} 的前 n 项和 Sn.