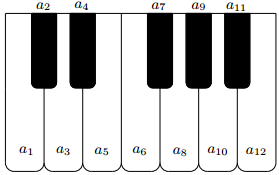
如图, 将钢琴上的 12 个键依次记为 a1, a2, · · · , a12, 设 1 ⩽ i ⩽ j ⩽ k ⩽ 12. 若 k − j = 3 且 j − i = 4, 则称 ai, aj, ak 为原位大三和弦; 若 k − j = 4 且 j − i = 3, 则称 ai, aj, ak 为原位小三和弦. 用这 12 个键可以构成的原 位大三和弦与原位小三和弦的个数之和为【 】
A、5
B、8
C、10
D、15
如图, 将钢琴上的 12 个键依次记为 a1, a2, · · · , a12, 设 1 ⩽ i ⩽ j ⩽ k ⩽ 12. 若 k − j = 3 且 j − i = 4, 则称 ai, aj, ak 为原位大三和弦; 若 k − j = 4 且 j − i = 3, 则称 ai, aj, ak 为原位小三和弦. 用这 12 个键可以构成的原 位大三和弦与原位小三和弦的个数之和为【 】

A、5
B、8
C、10
D、15
C
已知等差数列{an}的公差不为零,Sn为其前n项和,若S5=0,则Si (i=0,1,2,…,100)中不同的数值有________个。
已知方程(x2-2x+m)(x2-2x+n)=0的四个根组成一个首项为1/4的等差数列,则|m-n|=【 】
设正数数列{an },{bn}满足:a1=b1=1,bn=an bn-1-1/4(n≥2).求4+1/(a1 a2⋯ak )的最小值,其中m是给定的正整数.
等差数列{an}的各项均为正数,首项与公差相等,=2,则a4的值为【 】
在各项均为正数,且满足下列条件的数列{an}中,a9可能的最大值和最小值分别为M和m,则M+m的值为【 】(1) a7=40(2)对于任意正整数n,an+2=
数列{an },{bn}满足(3ak+5)=55,(ak+bk)=32,求bk 的值.
有半径为R之圆C,于其直径AB上取其半B1 B为直径作一圆C1,又取B1 B之半B2 B为直径作一圆C2,更取B2 B之半B3 B为直径作一圆C3,如是无限推之,求C1,C2,C3,⋯无穷个圆周之和.
Find the sum of n terms of the series whose nth term is 3(4n+4n²)-5n³.
Find the general term and the sum ofn terms of the series -3,-1,11,39,89,167.
Find the sum of the geometical series -2,,-1/3 to 6 terms.
求级数1/(1×3)+1/(3×5)+1/(5×7)+⋯ n项及无穷项之和.其第n项为1/(2n-1)(2n+1).