设正数数列{an },{bn}满足:a1=b1=1,bn=an bn-1-1/4(n≥2).
求4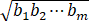 +
+ 1/(a1 a2⋯ak )的最小值,其中m是给定的正整数.
1/(a1 a2⋯ak )的最小值,其中m是给定的正整数.
设正数数列{an },{bn}满足:a1=b1=1,bn=an bn-1-1/4(n≥2).
求4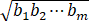 +
+ 1/(a1 a2⋯ak )的最小值,其中m是给定的正整数.
1/(a1 a2⋯ak )的最小值,其中m是给定的正整数.
由假设an=(bn+1/4)/bn-1 ,n≥2,于是a1 a2⋯an=((b2+1/4)(b3+1/4)⋯(bn+1/4))/(b1 b2⋯bn-1 ),即bn/(a1 a2⋯an )=bn/(a2⋯an )=(b2⋯bn)/((b2+1/4)(b3+1/4)⋯(bn+1/4))=1/((1+1/(4b2 ))(1+1/(4b3 ))⋯(1+1/(4bn )))≤又1/(a1 a2⋯ak )=1/a1 +1/(a1 a2⋯ak )=1+1/(a1 a2⋯a...
查看完整答案设数列 {an} 满足 a1 = 3, an+1 = 3an − 4n.(1) 计算 a2, a3, 猜想 {an} 的通项公式并加以证明;(2) 求数列 {2nan} 的前 n 项和 Sn.
将数列 {2n − 1} 与 {3n − 2} 的公共项从小到大排列得到数列 {an}, 则 {an} 的前 n 项和为 __________.
已知x1>0,x≠1,且xn+1=,(n=1,2,⋯).试证:数列{xn}或者对任意自然数n都满足xn<xn+1,或者对任意自然数n都满足xn>xn+1.
是否存在常数a,b,c使得等式1∙22+2∙32+⋯+n∙(n+1)2=(an2+bn+c)对一切自然数n都成立?并证明你的结论.
有四个数,其中前三个数成等差数列,后三个数成等比数列,并且第一个数与第四个数的和是16,第二个数与第三个数的和是12.求这四个数.
设{an}是首项为1的正项数列,且(n+1) - n+an+1an=0(n=1,2,3⋅⋅⋅),则它的通项公式是an=______.
设数列{an}的通项为an=2n-7(n∈N),则|a1|+|a2|+⋯+|a15|=______.
已知数列{an}满足a1=1,an+1=(1)记bn=a2n,写出b1,b2,并求数列{bn}的通项公式;(2)求{an}的前20项和.
数列{an}是递增的整数数列,且a1≥3,a1+a2+⋯+an=100,则n的最大值为【 】
已知ai∈N* (i=1,2,…,9)对任意的k∈N* (2≤k≤8),ak=ak-1+1或ak=ak+1-1中有且仅有一个成立,a1=6,a9=9,则a1+⋯+a9的最小值为__________.