设数列a1,a2,…,an,…的前n 项的和Sn与an的关系是Sn=-ban+1-1/(1+b)n ,其中b是与n无关的常数,且b≠1.
(1) 求an与an-1的关系;
(2) 写出用n和b表示an的表达式;
(3) 当0<b<1时,求极限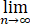 Sn .
Sn .
设数列a1,a2,…,an,…的前n 项的和Sn与an的关系是Sn=-ban+1-1/(1+b)n ,其中b是与n无关的常数,且b≠1.
(1) 求an与an-1的关系;
(2) 写出用n和b表示an的表达式;
(3) 当0<b<1时,求极限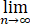 Sn .
Sn .
(1) an=Sn-Sn-1=-b(an-an-1 )-1/(1+b)n +1/(1+b)n-1 =-b(an-an-1 )+b/(1+b)n (n≥2),由此得an=b/(1+b) an-1+b/(1+b)n+1 (n≥2) ①(2) ∵ a1=S1=-ba1+1-1/(1+b),∴ a1=b/(1+b)2 . ②an=b/(1+b) [b/(1+b) an-2+b/(1+b)n ]+b/(1+b)n+1 =(b/(1+b))2 an-2+(b+b2)/(1+b)n+1 =(b/(1+b))2 [b/(1+b) an...
查看完整答案设复数z1和z2满足关系式=0,其中A为不等于0的复数.证明:(1)| z1+A||z2+A|=|A|2;(2) =||.
设对所有实数x,不等式x2log2 4(a+1)/a+2xlog2 2a/(a+1)+log2 (a+1)2/(4a2)>0恒成立,求a的取值范围.
如图,三棱锥P-ABC中,已知PA⊥BC,PA=BC=l,,PA,BC的公垂线,ED=h.求证:三棱锥P-ABC的体积V=l2h/6.
一个正三棱台的下底和上底的周长分别为30cm和12cm,且侧面积等于两底面积之差,求斜高.
由数字1,2,3,4,5组成没有重复数字且数字1与2不相邻的五位数,求这种五位数的个数.
在抛物线y=4x2上求一点,使该点到直线y=4x-5的距离最短.
求极限[1/(n2+1)+2/(n2+1)+3/(n2+1)+⋯2n/(n2+1)].
已知数列{an}满足:a1=1,a2=4,且an2 - an-1an+1=2n-1(n≥2,n∈N*),求a2020的个位数.
数列 {an} 满足 an+2 + (−1)nan = 3n − 1, 前 16 项和为 540, 则 a1 = ______.
数列 {an} 中, a1 = 2, am+n = aman , 若 ak+1 + ak+2 + · · · + ak+10 = 215 − 25, 则 k=【 】
设数列 {an} 满足 a1 = 3, an+1 = 3an − 4n.(1) 计算 a2, a3, 猜想 {an} 的通项公式并加以证明;(2) 求数列 {2nan} 的前 n 项和 Sn.
将数列 {2n − 1} 与 {3n − 2} 的公共项从小到大排列得到数列 {an}, 则 {an} 的前 n 项和为 __________.