已知 {an} 为等差数列, {bn} 为等比数列, a1 = b1 = 1, a5 = 5(a4 − a3), b5 = 4(b4 − b3).
(I) 求 {an} 和 {bn} 的通项公式;
(II) 记 {an} 的前 n 项和为 Sn, 求证: SnSn+2 < Sn+12 (n ∈ N∗);
(III) 对任意的正整数 n, 设 cn =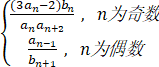 .求数列 {cn} 的前 2n 项和.
.求数列 {cn} 的前 2n 项和.
已知 {an} 为等差数列, {bn} 为等比数列, a1 = b1 = 1, a5 = 5(a4 − a3), b5 = 4(b4 − b3).
(I) 求 {an} 和 {bn} 的通项公式;
(II) 记 {an} 的前 n 项和为 Sn, 求证: SnSn+2 < Sn+12 (n ∈ N∗);
(III) 对任意的正整数 n, 设 cn =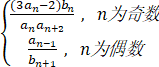 .求数列 {cn} 的前 2n 项和.
.求数列 {cn} 的前 2n 项和.
(I) 设等差数列 {an} 的公差为 d, 等比数列 {bn} 的公比为 q.由 a1 = 1, a5 = 5(a4 − a3), 可得 d = 1, 从而 {an} 的通项公式为 an = n.由 b1 = 1, b5 = 4(b4 − b3), 又 q≠ 0, 可得 q2 − 4q + 4 = 0, 解得 q = 2, 从而 {bn} 的通项公式为 bn = 2n−1.(II) 由 (I) 可得 Sn=n(n+1)/2 , 故 SnSn+2=1/4 n(n+1)(n+2)(n+3) , Sn+12=1/4 (n+1)2 (n+2)2 , 从而Sn Sn+2-Sn+12=-1/2 (n+1)(n+2)<0 所以, Sn Sn+2<Sn+12.(III) 当 n 为奇数时,cn=((3an-2)bn)/(anan+2) = = 2n+1/(n+2) - 2n-1/n当 n 为偶数时, cn=...
查看完整答案已知 a > 0, b > 0, 且 ab = 1, 则 1/(2a)+1/(2b)+8/(a+b)的最小值为_______.
已知甲、乙两球落入盒子的概率分别为 1/2和 1/3. 假定两球是否落入盒子互不影响, 则甲、乙两球都落入盒子的概率为______; 甲、乙两球至少有一个落入盒子的概率为______.
已知直线 x − y + 8 = 0 和圆 x2 + y2 = r2 (r > 0) 相交于 A, B 两点. 若 |AB| = 6, 则 r 的值为______.
在(x+2/x2 )5的展开式中, x2的系数是 ________.
i 是虚数单位, 复数 (8-i)/(2+i) = ________.
已知函数 f(x) =.若函数 g(x) = f(x) − |kx2 − 2x| (k ∈ R) 恰有 4 个零点, 则 k 的取值范围 是【 】.
设正数数列{an },{bn}满足:a1=b1=1,bn=an bn-1-1/4(n≥2).求4+1/(a1 a2⋯ak )的最小值,其中m是给定的正整数.
有半径为R之圆C,于其直径AB上取其半B1 B为直径作一圆C1,又取B1 B之半B2 B为直径作一圆C2,更取B2 B之半B3 B为直径作一圆C3,如是无限推之,求C1,C2,C3,⋯无穷个圆周之和.
Find the sum of n terms of the series whose nth term is 3(4n+4n²)-5n³.
Find the general term and the sum ofn terms of the series -3,-1,11,39,89,167.