已知椭圆 x2/a2 +y2/b2 =1 (a > b > 0) 的一个顶点为 A(0, −3), 右焦点为 F , 且 |OA| = |OF|, 其中 O 为原点.
(I) 求椭圆的方程;
(II) 已知点 C 满足 3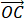 =
=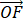 , 点 B 在椭圆上 (B 异于椭圆的顶点), 直线 AB 与以 C 为圆心的圆相切于点P , 且 P 为线段 AB 的中点. 求直线 AB 的方程.
, 点 B 在椭圆上 (B 异于椭圆的顶点), 直线 AB 与以 C 为圆心的圆相切于点P , 且 P 为线段 AB 的中点. 求直线 AB 的方程.
已知椭圆 x2/a2 +y2/b2 =1 (a > b > 0) 的一个顶点为 A(0, −3), 右焦点为 F , 且 |OA| = |OF|, 其中 O 为原点.
(I) 求椭圆的方程;
(II) 已知点 C 满足 3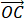 =
=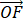 , 点 B 在椭圆上 (B 异于椭圆的顶点), 直线 AB 与以 C 为圆心的圆相切于点P , 且 P 为线段 AB 的中点. 求直线 AB 的方程.
, 点 B 在椭圆上 (B 异于椭圆的顶点), 直线 AB 与以 C 为圆心的圆相切于点P , 且 P 为线段 AB 的中点. 求直线 AB 的方程.
(I) 由己知可得 b = 3, 记半焦距为 c, 由 |OF| = |OA| 可得 c = b = 3. 又由 a2 = b2 + c2, 可得 a2 = 18.所以, 椭圆的方程为x2/18+y2/9=1.(II) 因为直线 AB 与以 C 为圆心的圆相切于点 P , 所以 AB ⊥ CP .依题意, 直线 AB 和直线 CP 的斜率均存在, 设直线 AB 的方程为 y = kx − 3.由方程组 , 消去 y, 可得 (2k2 + 1)x2 − 12kx = 0, 解得 x = 0, 或12k/(2k2+1) .依题意, 可得点 B 的坐标为 (12k/(2k2+1), (6...
查看完整答案双曲线之切线与渐近线相交,试证切点移动其所包围之三角形之面积为常数.
Reduce the hyperbola 4x² - 9y² - 24x + 36y - 36 = 0 to standard form.
于双曲线4/3 (x-2)2-(y+1)2=1中,已知其一直径之斜度为1/3,试求此直径及其共轭直径之方程式,若以此二共轭直径为新坐标轴,试求双曲线之新方程式.
若相相之二抛物线具有相同之顶点,且其主轴互相垂直,试证其公切线必与二抛物线各切于其通径之一端.
设 F 是抛物线的焦点,在抛物线上任取一点 P 与焦点连接,由 P 作 PQ平于主轴,试证 P 点的法线平分 ∠FPQ.
在直角坐标系xOy中,点P到x轴的距离等于点P到点(0,1/2)的距离,记动点P的轨迹为W.(1)求W的方程;(2)已知矩形ABCD有三个顶点在W上,证明:矩形ABCD的周长大于3√3.
设双曲线 C : x2/a2 − y2/b2 = 1 (a > 0, b > 0) 的一条渐近线为 y = x, 则 C 的离心率为______.
已知一圆经过二圆 x²+y² -2x +3y -7=0及x²+y²+3y -4=0 的交点及点(-2,1),求其方程.
堤上有塔高 50 尺,自堤下地面某点测得塔顶之仰角为 75°,塔底之仰角为 45°,求堤高.
△ABC 之底边 BC 的位置及长均为已知,自 B 至 AC 边之中线长亦为已知,求 A 点之轨迹.
求与 x =0,y = 0,3x +4y - 6 = 0 三线相切之圆的方程
已知在△ABC中,A+B=3C,2 sin(A-C)=sinB.(1)求sinA;(2)设AB=5,求AB边上的高.
过点(0,-2)与圆x²+y²-4x-1=0相切的两条直线的夹角为α,则sinα=【 】
已知在△ABC中,A+B=3C,2 sin(A-C)=sinB.(1)求sinA;(2)设AB=5,求AB边上的高.
已知直线l:x-my+1=0与⨀C:(x-1)²+y²=4交于A,B两点,写出满足“△ABC的面积为8/5”的m的一个值______.