已知Γ:x2/a2 +y2/b2 =1(a>b>0)的左、右焦点分别为F1 (-√2,0),F2 (√2,0),A为Γ的下顶点,M为直线l:x+y-4√2=0上一点.
(1)若a=2,AM的中点在x轴上,求点M的坐标;
(2)直线l交y轴于点B,直线AM经过点F2,若△ABM有一个内角的余弦值为3/5,求b;
(3)若椭圆Γ上存在点P到直线l的距离为d,且满足d+|PF1 |+|PF2 |=6,当a变化时,求d的最小值.
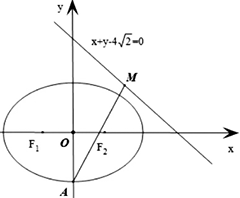
已知Γ:x2/a2 +y2/b2 =1(a>b>0)的左、右焦点分别为F1 (-√2,0),F2 (√2,0),A为Γ的下顶点,M为直线l:x+y-4√2=0上一点.

(1)若a=2,AM的中点在x轴上,求点M的坐标;
(2)直线l交y轴于点B,直线AM经过点F2,若△ABM有一个内角的余弦值为3/5,求b;
(3)若椭圆Γ上存在点P到直线l的距离为d,且满足d+|PF1 |+|PF2 |=6,当a变化时,求d的最小值.
(1)根据已知条件有,a=2,c=√2,b2=a2-c2=2,而A为Γ的下顶点,所以A的坐标为(0,-√2),设M(m,4√2-m),则AM的中点G(m/2,(4√2-√2-m)/2),由于G在x轴上,所以(4√2-√2-m)/2=0,解得m=3√2,∴M(3√2,√2).(2)若cosA=3/5,则tanA=4/3=√2/b,解得b=(3√2)/4;若...
查看完整答案抛物线y2 = 4x的弦AB垂直于x轴,若AB的长为4,则焦点到AB的距离为______。
抛物线y2 = 8 - 4x的准线方程是________,圆心在该抛物线的顶点且与其准线相切的圆的方程是____________.
如图,已知直线l过坐标原点,抛物线C的顶点在原点,焦点在x轴正半轴上.若点A(-1,0)和点B(0,8)关于l的对称点都在C上,求直线l和抛物线C的方程.
直线l过抛物线y2=a(x+1)(a>0)的焦点,并且与x轴垂直,若l被抛物线截得的线段长为4,则a=________.
已知双曲线x2/m - y2=1(m>0)的一条渐近线为 x+my=0,则C的焦距为________.
双曲线x2/4 - y2/5=1的右焦点到直线x+2y-8=0的距离为______.