已知 A, B 分别为椭圆 E :  +y2 = 1(a > 1) 的左、右顶点, G 为 E 的上顶点,
+y2 = 1(a > 1) 的左、右顶点, G 为 E 的上顶点, 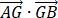 = 8, P 为直线 x = 6上的动点, PA 与 E 的另一交点为 C, PB 与 E 的另一交点为 D.
= 8, P 为直线 x = 6上的动点, PA 与 E 的另一交点为 C, PB 与 E 的另一交点为 D.
(1) 求 E 的方程;
(2) 证明: 直线 CD 过定点.
已知 A, B 分别为椭圆 E :  +y2 = 1(a > 1) 的左、右顶点, G 为 E 的上顶点,
+y2 = 1(a > 1) 的左、右顶点, G 为 E 的上顶点, 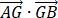 = 8, P 为直线 x = 6上的动点, PA 与 E 的另一交点为 C, PB 与 E 的另一交点为 D.
= 8, P 为直线 x = 6上的动点, PA 与 E 的另一交点为 C, PB 与 E 的另一交点为 D.
(1) 求 E 的方程;
(2) 证明: 直线 CD 过定点.
(1) 由题设得 A(−a, 0), B(a, 0), G(0, 1), 则 = (a, 1), = (a, −1) .由 · = 8 得 a2 − 1 = 8, 即 a = 3. 所以 E 的方程为 + y2 = 1.(2) 设 C(x1, y1), D(x2, y2), P (6, t).若 t ≠ 0, 设直线 CD 的方程为 x = my + n, 由题意可知 −3 < n < 3. 由于直线 PA 的方程为 y = (x + 3), 所以 y1 = (x1 + 3). 直线 PB 的方程为 y = (x − 3), 所以 y2 = (x2 − 3). 可得 3y1(x2 − 3) = y2(x1 + 3).由于+ = 1, 故 = − , 可得 27y1y2...
查看完整答案已知二次函数y=x2﹣6x+5.(1)求出它的图象的顶点坐标和对称轴方程;(2)画出它的图象;(3)分别求出它的图象和x轴、y轴的交点坐标.
已知O为坐标原点,点A(1,1)在抛物线C:x2=2py(p>0)上,过点B(0,-1)的直线交C于P,Q两点,则【 】
设F为抛物线C:y2=4x的焦点,点A在C上,点B(3,0),若|AF|=|BF|,则|AB|=【 】
设F为抛物线C:y2=4x的焦点,点A在C上,点B(3,0),若|AF|=|BF|,则|AB|=【 】
已知双曲线y2+x2/m=1的渐近线方程为y=±√3/3 x,则m=__________.
已知双曲线中心在原点,且一个焦点为F(√7,0),直线y=x-1与其相交于M,N两点,MN的中点横坐标为-2/3,则此双曲线的方程是【 】