高中数学-高考试题(河北省 1977年函数的极值与最值)

问答题（1977年河北省）

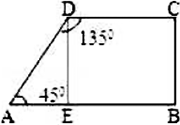
某生产队要建立一个形状是直角梯形的苗圃，其两邻边借用夹角为135°的两面墙，另外两边是总长为30米的篱笆(如图，AD和DC为墙)，问篱笆的两边各多长时，苗圃的面积最大？最大面积是多少？

答案解析

设BC长为x，苗圃面积为S.过D作DE⊥AB交AB于E.由已知条件可得AB=30-x,∠DAB=45°,AE=DE=BC=x,CD=BE=AB-AE=30-2x，∴S=1/2 (CD+AB)∙BC=1...

查看完整答案

讨论

高中数学

已知2lgx+lg2=lg⁡(x+6)，求x.

证明：(sin2α+1)/(1+cos2α+sin2α)=1/2 tanα+1/2.

如图，AB是⊙O的直径，CB是⊙O的切线，切点为B，OC平行于弦AD.求证：DC是⊙O的切线.

计算：sin 4π/3∙cos 25π/6∙tg(-3π/4).

分解因式x2y - 2y3.

河北省对数函数

计算：[1-(0.5)-2]÷(-27/8)1/3.

求函数y=1-的定义域.

河北省映射与函数

求椭园25x2+9y2=100的长轴和短轴的长、焦点坐标，并且画出它的图像。

函数的极值与最值

甲、乙两地相距s千米,汽车从甲地匀速行驶到乙地，速度不得超过c千米/时.已知汽车每小时的运输成本速度(以元为单位)由可变部分和固定部分组成:可变部分与速度v(千米/时)的平方成正比,比例系数为b;固定部分为a元.(Ⅰ)把全程运输成本y(元)表示为速度v(千米/时)的函数,并指出这个函数的定义域;(Ⅱ)为了使全程运输成本最小，汽车应以多大速度行驶?

如图,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱.污水从A孔流人,经沉淀后从B孔流出.设箱体的长度为a米,高度为b米.已知流出的水中该杂质的质量分数与a，b的乘积ab成反比.现有制箱材料60平方米.问:当a，b各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计)?

已知函数f(x)=(x2+2x+a)/x,x∈[1,+∞).当a=1/2时，求函数f(x)的最小值.

设a≠0，若x=a为函数f(x)=a(x-a)2(x-b)的极大值点，则【】

设(a-1)(b-1)>0,a,b,θ皆为实数，求(a+cosθ)(b+cosθ)/(1+cosθ)之极小值.

在测量某物理量的过程中,因仪器和观察的误差,使得n次测量分别得到a1,a2,…,an,共n个数据,我们规定所测量物理量的“最佳近似值”a是这样一个量:与其他近似值比较,a与各数据的差的平方和最小.依此规定,从a1,a2,…,an推出的a=____________.

设计一幅宣传画，要求画面面积为4840cm2，画面的宽与高的比为λ(λ<1)，画面的上、下各留8cm空白，左、右各留5cm空白，怎样确定画画的高与宽的尺寸，能使宣传画所用纸张面积最小？如果要求λ∈[2/3,3/4]，那么λ为何值时，能使宣传画所用的纸张面积最小？

下列函数中最小值为4的是【】

若a>0,b>0，则1/a+a/b2 +b的最小值为__________.

已知a>0，函数f(x)=ax-xex.(1)求函数y=f(x)在点(0,f(0))处的切点的方程；(2)证明函数f(x)存在唯一极值点；(3)若存在a，使得f(x)≤a+b对任意的x∈R成立，求实数b的取值范围.

函数

当a>1时，在同一坐标系中，函数y=a-x与y=loga⁡x的图像是【】

设f(x)是(-∞,+∞)上的奇函数, f(x+2)=-f(x)，当0≤x≤1时，f(x)=x，则f(7.5)等于【】

将y=2x的图像【】，再作关于直线y=x对称的图像,可得到函数y=log2⁡(x+1)的图像.

定义在区间(-∞,+∞)上的奇函数f(x)为增函数；偶函数g(x)在区间├ [0,+∞)上的图像与f(x)的图像重合.设a>b>0,给出下列不等式：①f(b)-f(-a)>g(a)-g(-b)；②f(b)-f(-a)<g(a)-g(-b)；③f(a)-f(-b)>g(b)-g(-a)；④f(a)-f(-b)>g(b)-g(-a).其中成立的是【】

函数y=a|x| (a>1)的图像是【】

函数f(x)=1/x (x≠0)的反函数f-1 (x)=【】

设曲线C的方程是y=x3 - x，将C沿x轴，y轴正向分别平行移动t,s单位长度后得曲线C1.(Ⅰ)写出曲线C1的方程；(Ⅱ)证明曲线C与C1关于点A(t/2,s/2)对称；(Ⅲ)如果曲线C与C1有且仅有一个公共点，证明s=t3/4 - t且t≠0.

若函数y=f(x)的反函数是y=g(x),f(a)=b,ab≠0，则g(b)等于【】

某蔬菜基地种植西红柿，由历年市场行情得知，从2月1日起的300天内，西红柿市场售价与上市时间的关系用图(左)的一条折线表示；西红柿的种植成本与上市时间的关系用图(右)的抛物线段表示.(I) 写出图(左)表示的市场售价与时间的函数关系式P=f(t);写出图(右)表示的种植成本与时间的函数关系式Q=g(t);(II) 认定市场售价减去种植成本为纯收益，问何时上市的西红柿纯收益最大？（注：市场售价和种植成本的单位：元/102kg,时间单位：天）

设集合A和B都是坐标平面上的点集{(x,y)|x∈R,y∈R},映射f:A→B把集合A中的元素（x,y）映射成集合B中的元素（x+y,x-y），则在映射f下，象(2,1)的原象是【】