在研究某市交通情况时, 道路密度是指该路段上一定时间内通过的车辆数除以时间, 车辆密度是该路段一定时间内通过的车辆数除以该路段的长度. 现定义交通流量为 v=q/x(x, q 分别是道路密度和车辆密度, 且 x ∈(0, 80]). 据调查某路段的交通流量有如下规律:
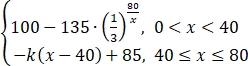 ,(k > 0).
,(k > 0).
求: (1) 若交通流量 v 大于 95, 求 x 的取值范围;
(2) 已知道路密度为 80 时, 交通流量为 50. 问 x 多少的时候 q 最大?
在研究某市交通情况时, 道路密度是指该路段上一定时间内通过的车辆数除以时间, 车辆密度是该路段一定时间内通过的车辆数除以该路段的长度. 现定义交通流量为 v=q/x(x, q 分别是道路密度和车辆密度, 且 x ∈(0, 80]). 据调查某路段的交通流量有如下规律:
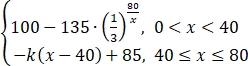 ,(k > 0).
,(k > 0).
求: (1) 若交通流量 v 大于 95, 求 x 的取值范围;
(2) 已知道路密度为 80 时, 交通流量为 50. 问 x 多少的时候 q 最大?
(1) 当 0 < x < 40 时, 100-135∙>95 , 有 x∈(0,80/3) .当 40 ⩽ x ⩽ 80 时, 由 k > 0, v ⩽ 85, 所以 v > 95 时, x∈(0,80/3) .(2) 当 x = 80, v = 50 代入原式可得 k=7/8 , 所以 v...
查看完整答案已知函数f(x)=cosαx-ln(1-x²),若x=0是f(x)的极大值点,求α的取值范围.
设(a-1)(b-1)>0,a,b,θ皆为实数,求(a+cosθ)(b+cosθ)/(1+cosθ)之极小值.
设函数f(x)满足:对任意非零实数x,均有f(x)=f(1)∙x+f(2)/x-1,则f(x)在(0,+∞)上的最小值为__________.
若a>0,b>0,则1/a+a/b2 +b的最小值为__________.
某生产队要建立一个形状是直角梯形的苗圃,其两邻边借用夹角为135°的两面墙,另外两边是总长为30米的篱笆(如图,AD和DC为墙),问篱笆的两边各多长时,苗圃的面积最大?最大面积是多少?