高中数学-高考试题(南京大学 1949年解方程)

计算题（1949年南京大学）

解方程组

答案解析

暂无答案

讨论

高中数学

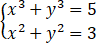
已知PA,PB,PC为过圆周上点P三弦，PT为圆之切线，设有一直线与PT平行，交PA,PB,PC于A',B',C'三点.求证：PA∙PA'=PB∙PB'=PC∙PC'.

已知角 A 及角内一点 P，求作过 P 点的直线，使其在 A 角内之部分被 P 点平分.

清华大学解方程

有连续三整数，其平方和为 50，求此三数.

求适合sin2x+cos2x=√2 sinx及0≤x≤2π的角的值.

求证：sin⁡(2nx)/(2nsinx)=cosx∙cos2x∙⋯∙cos⁡(2n-1x )

求证：3+4cosθ+cos2θ≥0

经过抛物线焦点的弦与抛物线的轴成角θ，试证此弦在抛物线内之截线等于L/sin²⁡θ ，其中L为正焦弦之长（经过焦点而又垂直于轴之弦，称为正焦弦）.

曲线xy=a²上一切线与坐标轴成一三角形，求此三角形的面积.

清华大学行列式

解方程

设f(x)是定义在区间(-∞,+∞)以2为周期的函数，对k∈Z，用Ik表示区间(2k-1,2k+1]，已知当x∈I0时，f(x)=x2.(Ⅰ)求f(x)在Ik上的解析表达式；(Ⅱ)对自然数k,求集合Mk={a|使方程f(x)=ax在Ik 上有两个不相等的实根}.

方程=1/4的解是【】

曲线2y2 + 3x + 3 = 0与曲线x2 + y2 - 4x - 5 = 0 的公共点的个数是【】

方程(1+3-x)/(1+3x)=3的解是______.

已知关于x的实系数二次方程x2+ax+b=0有两个实数根a,β.证明:(I)如果|α|<2,|β|<2,那么2|a|<4+b且|b|<4;(Ⅱ)如果2|a|<4+b且|b|<4,那么|α|<2,β|<2.

某地现有耕地10000公顷，规划10年后粮食单产比现在增加22%,人均粮食占有量比现在提高10%.如果人口年增长率为1%,那么耕地平均每年至多只能减少多少公顷(精确到1公顷)?

设二次函数f(x)=ax2+bx+c(a>0)，方程f(x) - x=0的两个根x1,x2满足0<x1<x2<1/a.(Ⅰ)当x∈(0,x1 )时，证明x<f(x)<x1；(Ⅱ)设函数f(x)的图像关于直线x=x0对称，证明x0<x1/2.

解x+y+=a,x-y+=b.

二水管齐开需72/7点钟装满一水池，若大管独开则较小管独开所需之时少 6点钟，试求每水管独开需若干点钟可装满此水池。

解下列方程式Ax2+2Bx+2(B-A)=0，并证明其根恒为实数.

函数

若2a=5b=10，则1/a+1/b=【】

已知a∈R，函数f(x)=，若f[f(√6)]=3，则a=__________.

求函数y=的定义域，并在数轴上表示出来.

求函数y=arcsin x/3的定义域，并在数轴上表示出来.

河北省映射与函数

求函数y=1-的定义域.

计算：[1-(0.5)-2]÷(-27/8)1/3.

将函数f(x)=ex展开为x的幂级数，并求出收敛区间.( e=2.718为自然对数)

化简下式：(1 - c2)-1/2 - {[(1+c)(1-c)]1/2+c2[(1+c)(1-c)]-1/2}.

某电管所为实现农业现代化，加強电力网的建设，沿着一条通往农村的新公路栽电线杆，已知一辆汽车每次从电管所运3根电线杆，相邻两根电线杆的距离为50米，汽车往返的总行程是35.5公里，最后一根电线杆与电管所的距离是2450米.(1)问第一根电线杆与电管所的距离是多少？(2)共栽了多少根电线杆？