高中数学-高考试题(中央大学 1947年解方程)

问答题（1947年中央大学）

解无理方程式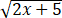+=，并就其结果讨论之.

答案解析

暂无答案

讨论

高中数学

设a1,a2,a3,⋯,an成调和级数，试证：a1 a2+a2 a3+a3 a4+⋯+an-1 an=(n-1) a1 an

设于椭圆上之 M(acosΦ,bsinΦ) 点，引与圆心 O之联线 OM，再由 M 点引正交于椭圆长轴之线 MP，复由 P引与 OM 正交之线 PQ.(1).求当 M 点沿圆线移动时 Q 点之轨迹.(2).讨论此轨迹之形状，并绘图以明之.

设有等边双曲线 (equilateral hyperbola) xy =1.今于其上取三点 A,B,C 联成三角形，而 A,B,C 之横标 (abscissa) 依次为 a,b,c.(1).求证过 △ABC 三顶点作向对边之垂线会于一点(2).求出三垂线之交点坐标，并证明此交点在双曲线上.

试述无穷级数为收敛或发散之定义 (definition of convergence or divergence)并讨论普遍项 (general term) 如下之二无穷级数，何时为收?何时为发散?(1) Un=xn+1 [log⁡(n+1) ]q(log 表以e 为底之对数)(2) Un=xn (cosn⁡θ+cosn-1⁡θ sinθ+cosn-2⁡θ sin2⁡θ+⋯+sinn⁡θ )(0<θ<π/4)

已知齐次方程组式中A,B,C为三参数.(1)求此方程组x=y=z=0之一组解答外，有其他解答时A,B,C间之关系.(2)求证A+B+C=π时，x,y,z恰为一三角形之三边.

设a,b,c为方程式x³+px+q=0之三根，Sn=an+bn+cn.(1)展开下列行列式为p,q之函数∆=(2)表明∆>0时，a,b,c为三个不同实根；∆<0时，a,b,c三根中有一为实根，其余为二相配虚根；∆=0时，a,b,c为三实根且至少有二根相等.

试解方程式 csc3θ + sec²θ = sinθcsc2θsec3θ.

以三角形各边为直径作圆，试证任意两边上二圆公切线之长为第三边被内切圆切点所分两部分之比例中项.

试求(1+2x+10x2)10之展开式中x5之系数.

某人每年存定款入银行，年利率依复利计算，若干年后得本利和恰为定款 3 倍设年数加倍.得本利和为定款之 5 倍，但取款时不存入定款，问年利率若干?

解方程

梨 10个柿8个较梨8个柿 10个少 30文，而梨柿各一个共钱 55 文，问梨柿每个价若干.

解1/(1+2x)-2/(2+3x)+3/(3+3x)-4/(4+4x)=0.

有甲、乙二书记，甲每写3页.乙能写4页，甲日写8点钟，10日之间已写 480页.问乙欲 15 日之力写完 720 页，每日须写几点钟.

武汉大学解方程

有甲、乙二列火车，甲列比乙列每点之速度多 15 里，如行36 里，则甲列比乙列先 12 分钟到，问甲、乙二列车之速度各几何.

英：If α,β,c are the roots of the equation x3-px2+qx-c=0, find the value of α2+β2+c2.汉：若α,β,c为x3-px2+qx-c=0的三个根，求 α2+β2+c2之值.

Solve the following equation by taking the steps performed in srriving at Cardann formulas, but do not formulas themselves: x³ - 15x² - 33x +847= 0.

试解方程式 a(x+y)= b(x - y) = xy

试解方程式(x+2)/(x-2)-(x-2)/(x+2)=5/6.

若x1,x2为方程式2x2-5x+3=0之二根，试求以x1/x2 与x2/x1 为根之方程式.

函数

设函数f(x)=若f(x)存在最小值，则a的一个取值为________；a的最大值为___________．

已知函数f(x)=，则f(f(1/2))=________；若当x∈[a,b]时，1≤f(x)≤3，则b-a的最大值是_________．

已知函数f(x)的定义域为[0,+∞)，且满足f(x)=f(1/(1+x))，记函数的值域为Af，若a>0，满足{y│y=f(x),x∈[0,a] }=Af，则实数a的取值范围为__________.

Let R+ denote the set of positive real numbers. Find all functions f:R⟶R such that for each x∈R+, there is exactly one y∈R+ satisfying：xf(y)+yf(x)≤2.译文：设R+表示所有正实数构成的集合.求所有函数f:R+→R+，使得对任意x∈R+，恰好有一个y∈R+满足条件：xf(y)+yf(x)≤2.

设函数f(x)=，若f(x0)>1，则x0的取值范围是【】

定义函数f(x)代表|x|-2与x2-ax+3a-5中较小的数.若f(x)至少有3个零点，则a的取值范围为__________.

若xi为大于1的整数，记f(xi)为xi的最大素因数.令xi+1=xi-f(xi)（i为自然数）.(1)证明：对任意大于1的整数x0，存在自然数k(x0)，使得xk(x0)+1=0;(2)令V(x0)为f(x0 ),f(x1 ),⋯,f(xk(x0))中不同的个数，求V(2),V(3),⋯,V(781)中的最大数，并说明理由.

有甲、乙两人，甲所有银为乙之五倍，其后甲得30元，乙得80元，则甲所有为乙之二倍，问甲、乙原各有银几何?

由甲地至乙地，若每时行 32 丈，则比预定时间迟2小时可到，若每小时行 56 丈，则比预定时间早1小时可到，问依预定时间每时应行之速?

北京工业大学映射与函数