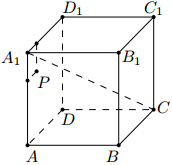
在棱长为 10 的正方体 ABCD − A1B1C1D1 中, P 为左侧面 ADD1A1 上一点, 已知点 P 到 A1D1 的距离为 3, 点 P 到 AA1 的距离为 2, 则过点 P 且与 A1C 平行的直线交正方体于 P、 Q 两点, 则 Q 点所在的平面是【 】
A、AA1B1B
B、BB1C1C
C、CC1D1D
D、ABCD
在棱长为 10 的正方体 ABCD − A1B1C1D1 中, P 为左侧面 ADD1A1 上一点, 已知点 P 到 A1D1 的距离为 3, 点 P 到 AA1 的距离为 2, 则过点 P 且与 A1C 平行的直线交正方体于 P、 Q 两点, 则 Q 点所在的平面是【 】

A、AA1B1B
B、BB1C1C
C、CC1D1D
D、ABCD
D
正三棱台高为1,上下底边长分别为3√3和4√3,所有顶点在同一球面上,则球的表面积是【 】
在长方体ABCD-A1B1C1D1中,已知B1D与平面ABCD和平面AA1B1B所成的角均为30°,则【 】
在正方体ABCD-A1B1C1D1中,E,F分别为AB,BC的中点,则【 】
已知球O的半径为1,四棱锥的顶点为O,底面的四个顶点均在球O的球面上,则当该四棱锥的体积最大时,其高为【 】
一个四面体的所有棱长都为√2,四个顶点在同一球面上,则此球的表面积为【 】
设正多面体每个顶点连有M条棱,每面都是正N边形,则正整数M和N满足关系:M>2,N>2,MN<2(M+N),这种正多面体共有【 】种。
有长方体积之冰块,其长 2 步,阔 1 步 3 尺,厚4 尺,而此冰之比重为 0.93,若置其于水中,浮出水面之高几寸?
下列物体中,能够被整体放入棱长为1(单位:m)的正方体容器(容器壁厚度忽略不计)内的有【 】
如图,长方体ABCD-A1 B1 C1 D1中,已知AB=BC=2,AA1=3. (1)若P是A1 D1上的动点,求三棱锥C-PAD的体积;(2)求直线AB1与平面ACC1 A1的夹角大小.
如图已知正方体ABCD-A1 B1 C1 D1,M,N分别是A1 D,D1 B的中点,则【 】
如图,已知长方体的对角线长为l,它与底面所成的角为α,底面两条对角线的夹角为β.求长方体的积体.
由正方体ABCD-A1B1C1D1的顶点A作该正方体的对角线A1C的垂线,垂足为E,证明A1E:EC=1:2.