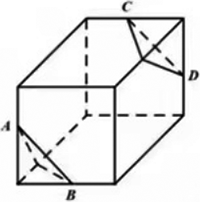
如图,从一个棱长为6米的正方体中裁去两个相同的正三棱锥，若正三棱锥的边长AB为4√2,则剩余何体的表面积为【 】
A、168
B、168+16√3
C、168+32√3
D、112+32√3
E、124+32√3
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
如图，PO是三棱锥P-ABC的高，PA=PB，AB⊥AC，E是PB的中点．（1）求证：OE//平面PAC；（2）若∠ABO=∠CBO=30°，PO=3，PA=5，求二面角C-AE-B的正弦值．
已知正三棱锥P-ABC的六条棱长均为6，S是△ABC及其内部的点构成的集合．设集合T={ Q∈S|PQ≤5}，则T表示的区域的面积为【 】
埃及胡夫金字塔是古代世界建筑奇迹之一, 它的形状可视为一个正四棱锥, 以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积, 则其侧面三角形底边上的高与底面正方形的边长的比值为 【】
如图，正三棱锥S-ABC的侧棱与底面边长相等，如果E,F分别为SC,AB的中点，那么异面直线EF与SA所成的角等于【 】
如果把两条异面直线看成“一对”，那么六棱锥的棱所在的12条直线中，异面直线共有【 】对。
如果三棱锥S-ABC的底面是不等边三角形，侧面与底面所成的二面角都相等，且顶点S在底面射影O在△ABC内，那么O是△ABC的【 】。
已知四棱锥的侧棱长为l，其各顶点都在同一球面上.若该球的体积为36π，且3≤l≤3√3，则该四棱锥体积的取值范围是【 】
在四棱锥P-ABCD中，PD⊥底面ABCD,CD//AB,AD=DC=CB=1,AB=2,DP=√3． （1）证明：BD⊥PA；（2）求PD与平面PAB所成的角的正弦值．
某三棱柱的底面为正三角形, 其三视图如图所示, 该三棱柱的表面积为【 】
某几何体的三视图 (单位: cm) 如图所示, 则该几何体的体积 (单位: cm3) 是【 】
如图, 六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的. 已知螺帽的底面正六边形边长为 2cm, 高 为 2cm, 内孔半径为 0.5cm, 则此六角螺帽毛坯的体积是 __________cm3.
如果正方体ABCD-A′B′C′D′的棱长为a，则A′-ABD的体积是【 】
如下图所示,在边长为4的正方形纸片ABCD中，AC与BD相交于O，剪去△AOB, 将剩余部分沿OC,OD折叠，使OA,OB重合，则A(B),C,DCO为顶点的四面体的体积是_______.
如图，正三棱锥S-ABC的侧面是边长为a的正三角形，D是SA的中点，E是BC的中点，求△SDE绕直线SE旋转一周所得到的旋转体的体积.
如图，三棱柱ABC-A1B1C1中，若E,F分别为AB,AC的中点，平面EB1C1F将三棱柱分成体积为V1,V2的两部分，那么V1:V2=__________.
如图，长方体ABCD-A1 B1 C1 D1中，已知AB=BC=2,AA1=3. (1)若P是A1 D1上的动点，求三棱锥C-PAD的体积；(2)求直线AB1与平面ACC1 A1的夹角大小.
如图已知正方体ABCD-A1 B1 C1 D1,M,N分别是A1 D,D1 B的中点，则【 】
如图，已知长方体的对角线长为l，它与底面所成的角为α，底面两条对角线的夹角为β.求长方体的积体.
由正方体ABCD-A1B1C1D1的顶点A作该正方体的对角线A1C的垂线，垂足为E，证明A1E:EC=1:2.
在长方体ABCD-A1B1C1D1中，已知B1D与平面ABCD和平面AA1B1B所成的角均为30°，则【 】
在正方体ABCD-A1B1C1D1中，E，F分别为AB,BC的中点，则【 】