如图,PO是三棱锥P-ABC的高,PA=PB,AB⊥AC,E是PB的中点.
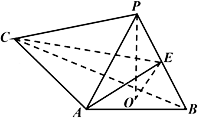
(1)求证:OE//平面PAC;
(2)若∠ABO=∠CBO=30°,PO=3,PA=5,求二面角C-AE-B的正弦值.
如图,PO是三棱锥P-ABC的高,PA=PB,AB⊥AC,E是PB的中点.

(1)求证:OE//平面PAC;
(2)若∠ABO=∠CBO=30°,PO=3,PA=5,求二面角C-AE-B的正弦值.
(1)证明:连接BO并延长交AC于点D,连接OA、PD,因为PO是三棱锥P-ABC的高,所以PO⊥平面ABC,AO,BO⊂平面ABC,所以PO⊥AO、PO⊥BO,又PA=PB,所以△POA≅△POB,即OA=OB,所以∠OAB=∠OBA,又AB⊥AC,即∠BAC=90°,所以∠OAB+∠OAD=90°,∠OBA+∠ODA=90°,所以∠ODA=∠OAD所以AO=DO,即AO=DO=OB,所以O为BD的中点,又E为PB的中点,所以OE// PD,又OE⊄平面PAC,PD⊂平面PAC,所以OE// 平面PAC.(2)过点A作Az// OP,如图建立平面直角坐标系,因为PO=3,AP=5,所以OA==4,又∠OBA=∠OBC=30°,所以BD=2OA=8,则AD=4,AB=4√3,所以AC=12,所以...
查看完整答案设三棱锥V-ABC中,∠AVB=∠BVC=∠CVA=直角.求证:ABC是锐角三角形.
如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,M为BC的中点,且PB⊥AM.(1) 证明:平面PAM⊥平面 PBD;(2) 若PD=DC=1,求四棱锥P-ABCD 的体积.
如图,三棱锥P-ABC中,已知PA⊥BC,PA=BC=l,,PA,BC的公垂线,ED=h.求证:三棱锥P-ABC的体积V=l2h/6.
如图,正三棱锥S-ABC的侧棱与底面边长相等,如果E,F分别为SC,AB的中点,那么异面直线EF与SA所成的角等于【 】
如果把两条异面直线看成“一对”,那么六棱锥的棱所在的12条直线中,异面直线共有【 】对。
如果三棱锥S-ABC的底面是不等边三角形,侧面与底面所成的二面角都相等,且顶点S在底面射影O在△ABC内,那么O是△ABC的【 】。
已知正六棱台的上、下底面边长分别为2和4,高为2,则其体积为【 】
如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,AF⊥DE,F是垂足.(1)求证:AF⊥DB;2)如果圆柱与三棱锥D-ABE的体积比等于3πr,求直线DE与平面ABCD所成的角.
圆台上、下底面积分别为π,4π侧面积为6π,这个圆台的体积是【 】
向高为H的水瓶中注水,注满为止.如果注水量V与水深h的函数关系的图像如图所示,那么水瓶的形状是【 】
如图,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF//AB,EF=3/2,EF与面AC的距离为2,则该多面体的体积为【 】
若一个圆锥的轴截面是等边三角形,其面积为,则这个圆锥的侧面积是________.
若一个圆锥的轴截面是等边三角形,其面积为,则这个圆锥的全面积是【 】
已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为【 】
两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为32π/3,两个圆锥的高之比为1:3,则这两个圆锥的体积之和为【 】
如图, 在正方体 ABCD − A1B1C1D1 中, E 为 BB1 的中点.(I) 求证: BC1 // 平面 AD1E;(II) 求直线 AA1 与平面 AD1E 所成角的正弦值.
如图,已知二面角α-AB-β的平面角是锐角,C是平面α内的一点(它不在棱AB上),点D是点C在平面β上的射影,点E是棱AB上满足∠CEB为锐角的任意一点,那么【 】.
如图,四棱锥S-ABCD的底面是边长为1的正方形,侧棱SB垂直于底面,并且SB=,用α表示∠ASD,求sinα的值.
如图,在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC.DE垂直平分SC,且分别交AC,SC于D,E.又SA=AB,SB=BC.求以BD为棱,以BDE与BDC为面的二面角的度数.