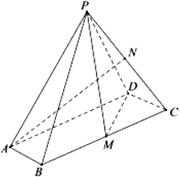
如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，∠ABC=120°,AB=1,BC=4,PA=
,M,N分别为BC,PC的中点PD⊥DC,PM⊥MD.
(1)证明：AB⊥PM;
(2)求直线AN与平面PDM所成角的正弦值.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
问答题（2021年浙江省）
答案解析
(1)在△DCM中，DC=1,CM=2,∠DCM=60°,由余弦定理可得DM=√3.∴DM2+DC2=CM2,∴DM⊥DC.由题意DC⊥PD且PD∩DM=D，∴DC⊥平面PDM,∵PM⊂平面PDM，∴DC⊥PM,∵AB//DC，∴AB⊥PM.(2)∵PM⊥MD,AB⊥PM,且AB与DM相交，∴PM⊥平面ABCD.在△ABM中,解得在AM=√7，∴PM=2√2取AD的中点E，连接ME，...
查看完整答案讨论
将边长为a的正方形ABCD沿对角线AC折起,使得BD=a,,则三棱锥D-ABC的体积为【 】
已知三棱锥D-ABC的三个侧面与底面全等，且AB=AC=,BC=2，则以BC为棱，以面BCD与面BCA为面的二面角的大小是【 】
在正三棱锥ABC-A1B1C1中，若AB=BB1，则AB1与C1B所成的角的大小为【 】
如图,在底面是直角梯形的四棱锥S-ABCD中，∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=1/2. (I)求四棱锥S-ABCD的体积;(Ⅱ)求面SCD与面SBA所成二面角的正切值.
如图，四棱锥P-ABCD的底面是矩形，PD⊥底面ABCD，M为BC的中点，且PB⊥AM．(1) 证明：平面PAM⊥平面 PBD；(2) 若PD=DC=1，求四棱锥P-ABCD 的体积.
埃及胡夫金字塔是古代世界建筑奇迹之一, 它的形状可视为一个正四棱锥, 以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积, 则其侧面三角形底边上的高与底面正方形的边长的比值为 【】
已知圆锥的中截面周长为a，母线长为l，则它的侧面积等于______.
已知圆台的上、下底面半径分别为r，2r，侧面积等于上、下底面积之和，则圆台的高为_______.
长方体的全面积为11,12条棱长度之和为24,则这个长方体的一条对角线长为【 】
在半径为30m的圆形广场中央上空，设置一个照明光源，射向地面的光呈圆锥形，且其轴截面顶角为120°。若要光源恰好照亮整个广场，则其高度应为________(精确到0.1m)。
建造一个容积为8m3，深为2m的长方体无盖水池。如果池底和池壁的造价每平方米分别为120元和80元，那么水池的最低总造价为________元。
设圆锥底面圆周上两点A,B间的距离为2,圆锥顶点到直线AB的距离为,AB和圆锥的轴的距离为1,则该圆锥的体积为________.
如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,AF⊥DE,F是垂足.(1)求证:AF⊥DB;2)如果圆柱与三棱锥D-ABE的体积比等于3πr,求直线DE与平面ABCD所成的角.
如图，AB是圆O的直径，PA垂直于圆O所在的平面，C是圆周上不同于A，B的任意一点.求证：平面PAC垂直于平面PBC.
如图，正四棱台中，A'D'所在的直线与BB'所在的直线是【 】
如图，已知圆柱的底面半径是3，高是4，A，B两点分别在两底面的圆周上，并且AB=5，那么直线AB与轴oo'之间的距离等于______.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是【 】
已知：两条异面直线a,b所成的角为θ，它们的公垂线段AA1的长度为d.在直线a,b上分别取点E,F，设A1E=m,AF=n. 求证：EF=.
已知异面直线a与b所成的角为50°，P为空间一定点，则过点P且与a、b所成的角都是30°的直线有且仅有【 】
如果直线l，m与平面α，β，γ满足：l=β∩γ,l//α,m⊂α和m⊥γ，那么必有【 】
如图,正方形ABCD所在平面与正方形ABEF所在平面成60°的二面角,则异面直线AD与BF所成角的余弦值是________.
如图所示四面体A-BCD中，AB,BC,BD两两互相垂直，且AB=BC=2，E是AC的中点，异面直线AD与BE所成的角大小为arccos /10，求四面体A-BCD的体积.