已知一级数第n项为lg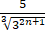
，试求此级数前几项之和.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
试从x=by+cz,y=cz+ax,z=ax+by，消去x,y,z.求a,b,c间的关系式.
方程12x³-28x²+17x-3=0之根为a,b,c，已知b=a+1，求a,b,c.
证明： cos(α+β-γ)+cos(α-β+γ)-cos(β+γ-α)-cos(α+β+γ)=4cosα∙sinβ∙sinγ.
设人眼在墙顶上观察一塔，测得塔之全长所夹之角为θ，设墙高为h尺，墙与塔之距离为d尺.试证：(h²+d²)sinθ/(hsinθ+dcosθ)尺为塔这高.
试判别方程x²+2xy-8y²+2x+14y-3=0之图形的性质.
一圆经过两点(2,-3),(-4,-1)，而其中心在直线3y+x-18=0上，求圆的方程.
试证arcsinx+arcsiny=arcsin(x+y).
设α,β,γ为三角形内角，求证tg(α/2)∙tg(β/2)+tg(β/2)∙tg(γ/2)+tg(γ/2)∙tg(α/2)=1.
已知{an}是等比数列，如果a1+a2+a3=18,a2+a3+a4=-9，且Sn=a1+a2+⋯+an，那么Sn 的值等于【 】
已知{an}是公差不为零的等差数列，如果Sn是{an}的前n项和，那么(nan)/Sn )等于______.
有四个数，其中前三个数成等差数列，后三个数成等比数列，并且第一个数与第四个数的和是16，第二个数与第三个数的和是12.求这四个数.
[n(1-1/3)(1-1/4)(1-1/5)…(1-1/(n+1))]的值等于【 】
等差数列{an},{bn}的前n项和分别为Sn与Tn，若Sn/Tn =2n/(3n+1)，则an/bn 等于【 】
等比数列{an}的首项a1=-1，前n项和为Sn，若S10/S5 =31/32,则Sn 等于【 】
已知数列{an }，{bn }都是由正数组成的等比数列，公比分别为p,q，其中p>q且p≠1,q≠1，设cn= an+bn，Sn为数列{cn}的前n项和.求Sn/Sn-1 .
设{an}是首项为1的正项数列，且(n+1) - n+an+1an=0(n=1,2,3⋅⋅⋅),则它的通项公式是an=______.
设数列{an}的通项为an=2n-7(n∈N)，则|a1|+|a2|+⋯+|a15|=______.
已知数列{an}满足a1=1,an+1=(1)记bn=a2n，写出b1,b2，并求数列{bn}的通项公式；(2)求{an}的前20项和.
数列{an}是递增的整数数列，且a1≥3,a1+a2+⋯+an=100，则n的最大值为【 】
已知ai∈N* (i=1,2,…,9)对任意的k∈N* (2≤k≤8),ak=ak-1+1或ak=ak+1-1中有且仅有一个成立，a1=6,a9=9，则a1+⋯+a9的最小值为__________.