已知数列{an}满足a1=1,an+1=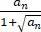 (n∈N* ).记{an}的前n项和为Sn,则【 】
(n∈N* ).记{an}的前n项和为Sn,则【 】
A、1/2<S100<3
B、3<S100<4
C、4<S100<9/2
D、9/2<S100<5
已知数列{an}满足a1=1,an+1=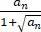 (n∈N* ).记{an}的前n项和为Sn,则【 】
(n∈N* ).记{an}的前n项和为Sn,则【 】
A、1/2<S100<3
B、3<S100<4
C、4<S100<9/2
D、9/2<S100<5
A
等差数列{an},{bn}的前n项和分别为Sn与Tn,若Sn/Tn =2n/(3n+1),则an/bn 等于【 】
等比数列{an}的首项a1=-1,前n项和为Sn,若S10/S5 =31/32,则Sn 等于【 】
已知数列{an },{bn }都是由正数组成的等比数列,公比分别为p,q,其中p>q且p≠1,q≠1,设cn= an+bn,Sn为数列{cn}的前n项和.求Sn/Sn-1 .
在等比数列{an}中,a1>1,且前n项和Sn满足Sn=1/a1 ,那么a1的取值范围是【 】
已知等差数列前三项为a,4,3a前n项的和为Sn,Sk=2550.(Ⅰ)求a及k的值,(Ⅱ)求 (1/S1 +1/S2 +⋯+1/Sn ).
极限(C22+C32+C42+⋯+Cn2)/(n(C21+C31+C41+⋯+Cn1))=【 】
已知数列{an}满足an+1=1/4 (an-6)³+6(n=1,2,3,⋯),则【 】
令S=m²n/(2m(n2m+m2n)),则[100S]=________.
已知数列{an}满足:a1=1,a2=4,且an2 - an-1an+1=2n-1(n≥2,n∈N*),求a2020的个位数.
数列 {an} 满足 an+2 + (−1)nan = 3n − 1, 前 16 项和为 540, 则 a1 = ______.
数列 {an} 中, a1 = 2, am+n = aman , 若 ak+1 + ak+2 + · · · + ak+10 = 215 − 25, 则 k=【 】
设数列 {an} 满足 a1 = 3, an+1 = 3an − 4n.(1) 计算 a2, a3, 猜想 {an} 的通项公式并加以证明;(2) 求数列 {2nan} 的前 n 项和 Sn.
将数列 {2n − 1} 与 {3n − 2} 的公共项从小到大排列得到数列 {an}, 则 {an} 的前 n 项和为 __________.