已知a₁,a₂,⋯,a_n为实数，且∑_i=1ⁿa_i =n,∑_i=1ⁿa_i² =2n,∑_i=1ⁿa_i³ =3n.

(1)求最大的常数C，使得对所有n≥3，均有max⁡{a₁,a₂,⋯,a_n }-min⁡{a₁,a₂,⋯,a_n }≥C；

(2)证明存在常数C₂>0使得max⁡{a₁,a₂,⋯,a_n }-min⁡{a₁,a₂,⋯,a_n }+C≥C₂^n-3，其中C为(1)中的常数.

给定无理数α>1,L∈Z，满足L>α²/(α-1)，数列{x_n}满足x₁>L，且

x_n+1=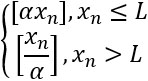

(1)证明：{x_n}最终周期；

(2)证明：{x_n}最终的最小正周期是一个与x₁无关的奇数.

设a₁,a₂,a₃,⋯是一个无穷项的正整数序列，且N是一下正整数.已知对任意整数n>N,a_n等于a_n-1在a₁,a₂,⋯,a_n-1中出现的次数.

证明：序列a₁,a₃,a₅,⋯与序列a₂,a₄,a₆,⋯两者至少有一个是最终周期的.

(一个无穷项的序列b₁,b₂,b₃,⋯称为最终周期的，如果存在正整数p和M使得b_m+p=b_m对所有整数m≥M均成立)

已知数列{a_n}是公比大于0的等比数列，其前n项和为S_n，且a₁=1,S₂=a₃-1.

(1)求数列{a_n}的前n项和S_n；

(2)设b_n=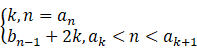,b₁=1，其中k是大于1的正整数.

(ⅰ)当n=a_k+1时，求证：b_n-1≥a_k∙b_k；

(ⅱ)求∑_i=1^Snb_i .

等比数列{a_n}的首项a₁>0，公比q>1，记I_n={x-y│x,y∈[a₁,a₂ ]∪[a_n,a_n+1 ] }，若对任意正整数n,I_n是闭区间，则q的取值范围是________.