高中数学-高考试题(全国统考 1987年抛物线)

问答题（1987年全国统考）

在抛物线y=4x²上求一点，使该点到直线y=4x-5的距离最短.

答案解析

设P(x,y)为抛物线上任一点，则该点到直线y=4x-5的距离

d==

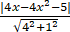
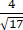=(x²-x+5/4)=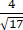[(x-1/2)²+1]

从而，当x=1/2时，d有最小值，此时P点的坐标为(1/2,1).

讨论

抛物线

Given the parabola y²=4x and the line x=2+ecosα,y=-4+ecosβ，find the condition which cosα and cosβ must satisfy if the line meets the parabola in but one point.

试证在抛物线正焦弦两端点所作切线互相垂直，又若此抛物线之方程式为x²=2px，试求其在上述二切线为坐标轴时之新方程式.

F 点为抛物线 y² = 16x 之焦点，O 点为顶点，P 点为抛物线上任一点，PQ 为切线，自 O 点至 PQ 线之垂线与 FP 线相交 R 点，求 R 点之轨迹之方程式并绘其图形.

Show that the tangents to the parabola y² = 4px at the extremities of the latus return are perpendicular and meet at the intersection of the directrix with a-axis.

从点(-8,8)引 2xy +y² =8 的两条切线，求它们的夹角.

若相相之二抛物线具有相同之顶点，且其主轴互相垂直，试证其公切线必与二抛物线各切于其通径之一端.

设 F 是抛物线的焦点，在抛物线上任取一点 P 与焦点连接，由 P 作 PQ平于主轴，试证 P 点的法线平分 ∠FPQ.

在直角坐标系xOy中，点P到x轴的距离等于点P到点(0,1/2)的距离，记动点P的轨迹为W.(1)求W的方程；(2)已知矩形ABCD有三个顶点在W上，证明：矩形ABCD的周长大于3√3.

抛物线y2=2px的内接三角形有两边与抛物线x2=2qy相切，证明这个三角形的第三边也与抛物线x2=2qy相切.

若动点P到F(2,0)的距离与它到直线x+2=0的距离相等，则点P的轨迹方程为___________.

圆锥曲线

已知椭圆x2/6+y2/3=1，直线l与椭圆在第一象限交于A，B两点，与x轴，y轴分别交于M，N两点，且|MA|=|NB|,|MN|=2√3，则直线l的方程为___________．

椭圆C:x2/a2 +y2/b2 =1(a>b>0)的左顶点为A，点P，Q均在C上，且关于y轴对称．若直线AP,AQ的斜率之积为1/4，则C的离心率为【】

已知椭圆C:x2/a2 +y2/b2 =1(a>b>0)的离心率为1/3，A1,A2分别为C的左、右顶点，B为C的上顶点．若(BA1)⋅(BA2)=-1，则C的方程为【】

已知椭圆E的中心为坐标原点，对称轴为x轴、y轴，且过A(0,-2),B(3/2,-1)两点．（1）求E的方程；（2）设过点P(1,-2)的直线交E于M，N两点，过M且平行于x轴的直线与线段AB交于点T，点H满足(MT)→=(TH)→．证明：直线HN过定点.

已知椭圆： E:x2/a2 +y2/b2 =1(a>b>0)的一个顶点为A(0,1)，焦距为2√3．（1）求椭圆E的方程；（2）过点P(-2,1)作斜率为k的直线与椭圆E交于不同的两点B，C，直线AB，AC分别与x轴交于点M，N，当|MN|=2时，求k的值．

如图，已知椭圆x2/12+y2=1．设A，B是椭圆上异于P(0,1)的两点，且点Q(0,1/2)在线段AB上，直线PA,PB分别交直线y=-1/2 x+3于C，D两点．（1）求点P到椭圆上点的距离的最大值；（2）求|CD|的最小值．

已知Γ:x2/a2 +y2/b2 =1(a>b>0)的左、右焦点分别为F1 (-√2,0),F2 (√2,0),A为Γ的下顶点，M为直线l:x+y-4√2=0上一点.(1)若a=2,AM的中点在x轴上，求点M的坐标；(2)直线l交y轴于点B，直线AM经过点F2，若△ABM有一个内角的余弦值为3/5，求b；(3)若椭圆Γ上存在点P到直线l的距离为d，且满足d+|PF1 |+|PF2 |=6，当a变化时，求d的最小值.

已知常数a>0，在矩形ABCD中，AB=4,BC=4a,O为AB的中点，点E,F,G分别在BC,CD,DA上移动，且BE/BC=CF/CD=DG/DA,P为GE与OF的交点(如图).问是否存在两个定点，使P到这两点的距离的和为定值?若存在，求出这两点的坐标及此定值;若不存在，请说明理由.

已知椭圆方程x2/a2 +y2/b2 =1,F为右焦点，A为右顶点，B为上顶点，|BF|/|AB| =√3/2.(1)求椭圆的离心率e；(2)已知直线l与椭圆有唯一交点M，直线l交y轴于点N,|OM|=|ON|,∆OMN的面积为√3,求椭圆的标准方程.

定义椭圆x2/a2 +y2/b2 =1的辅助圆为x2+y2=a2.考虑椭圆x2/4+y2/3=1，点H(a,0),0<a<2. 在第一象限内，过H平行于y轴的直线与椭圆交于点E，与椭圆的辅助圆交于点F，椭圆在点E处的切线与x轴正半轴交于点G，过原点和F的直线与x轴正半轴的夹角为φ.列Ⅰ 列Ⅱ(Ⅰ)若φ=π/4，则△FGH的面积为 (P) (√3-1)4/8(Ⅱ)若φ=π/3，则△FGH的面积为 (Q) 1(Ⅲ)若φ=π/6，则△FGH的面积为 (R) 3/4(Ⅳ)若φ=π/12，则△FGH的面积为 (S) 1/(2√3) (T) (3√3)/2正确的选项为【】

平面解析几何

在边长为1的等边三角形ABC中，D为线段BC上的动点，DE⊥AB且交AB于点E,DF//AB交AC于点F，则|2+|的值为__________；(+)∙最小值为__________.

在△ABC中，角A,B,C所对的边分别为a,b,c.已知sinA:sinB:sinC=2:1:√2,b=√2.(1)求a的值；(2)求cosC的值；(3)求sin⁡(2C-π/6)的值.

已知△ABC，若对任意t∈R,|(BA)→-t(BC)→ |≥|(AC)→|，则△ABC一定为【】。

在△ABC中，点D在边AB上，BD=2DA.记=m,=n，则=【】

已知a→=(3,4),b→=(1,0),c→=a→+tb→，若<a→,c→>=<b→,c→>，则t=【】

设向量a，b的夹角的余弦值为1/3，且|a|=1，|b|=3，则(2a+b)⋅b=_________．

已知△ABC中，点D在边BC上，∠ADB=120°,AD=2,CD=2BD．当AC/AB取得最小值时，BD=________．

已知向量a=(m,3),b=(1,m+1)．若a⊥b，则m=__________．

在△ABC中，角A，B，C所对的边分别为a，b，c．已知4a=√5 c,cos⁡C=3/5．（1）求sin⁡A的值；（2）若b=11，求△ABC的面积．

已知λ>0，向量|a|=|b|=|c|=λ，且a∙b=0,c∙b=1,c∙a=2，则λ=________.