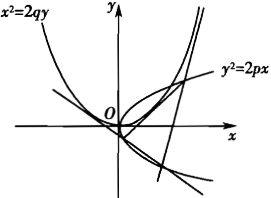
抛物线y2=2px的内接三角形有两边与抛物线x2=2qy相切,证明这个三角形的第三边也与抛物线x2=2qy相切.
抛物线y2=2px的内接三角形有两边与抛物线x2=2qy相切,证明这个三角形的第三边也与抛物线x2=2qy相切.

不失一般性,设p>0,q>0.又设y2=2px的内接三角形顶点为A1 (x1,y1 ),A2 (x2,y2 ),A3 (x3,y3).因此 y12=2px1,y22=2px2,y32=2px3.其中,y1≠y2,y2≠y3,y3≠y1.依题意,设A1,A2,A3与抛物线x2=2qy相切. 因为x2=2qy在原点O处的切线是y2=2px的对称轴,所以原点O不能是所设内接三角形的顶点,即(x1,y1 ) ,(x2,y2 ),(x3,y3)都不能是(0,0).又因为A1 A2与x2=2qy相切,所以A1 A2不能与y轴平行,即x1≠x2,y1≠-y2,直线A1 A2的方程为y-y1=(y2-y1)/(x2-x1 )(x-x1),∵y22-y12=(y2-y1 )(y2+y1 )=2p(x2-x1),∴A1 A2的方程是y=2p/(y1+y2 ) x+(y1 y2)/(y1+y2 ).A1 A2与抛物线x2=2qy交点的横坐标满...
查看完整答案从点(-8,8)引 2xy +y² =8 的两条切线,求它们的夹角.
若相相之二抛物线具有相同之顶点,且其主轴互相垂直,试证其公切线必与二抛物线各切于其通径之一端.
设 F 是抛物线的焦点,在抛物线上任取一点 P 与焦点连接,由 P 作 PQ平于主轴,试证 P 点的法线平分 ∠FPQ.
在直角坐标系xOy中,点P到x轴的距离等于点P到点(0,1/2)的距离,记动点P的轨迹为W.(1)求W的方程;(2)已知矩形ABCD有三个顶点在W上,证明:矩形ABCD的周长大于3√3.
直线l过抛物线y2=a(x+1)(a>0)的焦点,并且与x轴垂直,若l被抛物线截得的线段长为4,则a=________.
已知圆x2 + y2 - 6x - 7 = 0与抛物线y2 = 2px(p>0)的准线相切,则p=________.
设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线与A,B两点,点C在抛物线的准线上,且BC//x轴.证明AC经过原点O.
已知O为坐标原点,过抛物线C:y2=2px(p>0)的焦点F的直线与C交于A,B两点,点A在第一象限,点M(p,0),若|AF|=|AM|,则【 】
曲线y=(2x-1)/(x+2)在点(-1,-3)处的切线方程为__________.
已知向量=(3,1),=(1,0),=+k,若⊥,则k=________.
记△ABC的内角A,B,C的对边分别为a,b,c,面积为,B=60°,a2+c2=3ac,则b=______.
已知向量=(2,5),=(λ,4),若//,则λ=_______.
已知a=(2,1),b=(2,-1),c=(0,1),则(a+b)·c=______;a·b=______.
在边长为1的等边三角形ABC中,D为线段BC上的动点,DE⊥AB且交AB于点E,DF//AB交AC于点F,则|2+|的值为__________;(+)∙最小值为__________.