在 △ABC 中, AB = 4, AC = 3, ∠BAC = 90º, D 在边 BC 上, 延长 AD 到 P , 使得 AP = 9. 若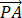 =m
=m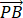 +(3/2-m)
+(3/2-m)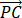 (m 为常数), 则 CD 的长度是__________.
(m 为常数), 则 CD 的长度是__________.
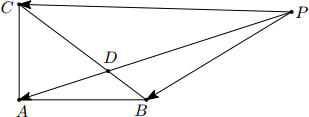
在 △ABC 中, AB = 4, AC = 3, ∠BAC = 90º, D 在边 BC 上, 延长 AD 到 P , 使得 AP = 9. 若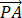 =m
=m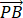 +(3/2-m)
+(3/2-m)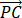 (m 为常数), 则 CD 的长度是__________.
(m 为常数), 则 CD 的长度是__________.

18/5或 0.
已知 5x2y2 + y4 = 1 (x, y ∈ R), 则 x2 + y2 的最小值是________.
将函数y=3sin(2x+π/4)的图象向右平移 π/6 个单位长度, 则平移后的图像中与 y 轴最近的对称轴的方程是__________.
如图, 六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的. 已知螺帽的底面正六边形边长为 2cm, 高 为 2cm, 内孔半径为 0.5cm, 则此六角螺帽毛坯的体积是 __________cm3.
已知sin2(π/4+α)=2/3, 则sin2α的值是_______.
已知 y = f(x) 是奇函数, 当 x ⩾ 0 时, f(x) = x2/3 , 则 f(−8) 的值是______.
在平面直角坐标系 xOy 中, 若双曲线 x2/a2 -y2/5=1 (a > 0) 的一条渐近线方程为 y=/2 x , 则该双曲线的 离心率是_______.
如图是一个算法流程图, 若输出 y 的值为 −2, 则输入 x 的值是______.
已知向量a ̅=(1,1),b ̅=(1,-1).若(a ̅+λb ̅)⊥(a ̅+μb ̅),则【 】
已知向量a→,b→满足|a→-b→ |=√3,|a→+b→ |=|2a→-b→|,则|b→ |=________.
已知向量a→,b→满足a→+b→=(2,3),a→-b→=(-2,1),则|a→ |²-|b→ |²=【 】
已知向量|a➝ |=1,|b➝ |=2,且a➝,b➝的夹角为120°.若a➝+tb➝与ta➝+b➝的夹角为锐角,则t的取值范围是__________.
已知向量a ̅=(0,1),b ̅=(2,x),若b ̅⊥(b ̅- 4a ̅),则x=【 】
设向量 a = (1, −1), b = (m + 1, 2m − 4), 若 a ⊥ b, 则 m =______ .
己知单位向量 a, b 的夹角为 45°, ka − b 与 a 垂直, 则 k = ______.
已知单位向量 a, b 的夹角为 60°, 则下列向量中, 与 b 垂直的是【 】
设有一三角形ABC:假定A及B两顶为固定不移,其他一C在AC²+BC²=2/5 AB²之条件下运动,则其轨迹为何如?
两树相距 50 尺,在此树距地 5 尺处观他树之树顶与树根适成 90°之角,又观他树顶之仰角为 60°,求他树之高.
求已知圆 x²+y² - 6x +4y = 12 之两切方程式,与一已知线 4x + 3y +5=0平行.
某人在高处望见正东海面上一船首,其俯角为 30°,当船向正南行 a 里后,求得船首俯角为 15°,问此人之视点高出海面若干?
若 kxy - 8x + 9y - 12 = 0 表示二条直线,求 k 值及此二直线所夹的角.