已知 P 是边长为 2 的正六边形 ABCDEF 内的一点, 则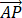 •
•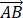 的取值范围是【 】
的取值范围是【 】
A、(−2, 6)
B、(−6, 2)
C、(−2, 4)
D、(−4, 6)
已知 P 是边长为 2 的正六边形 ABCDEF 内的一点, 则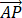 •
•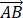 的取值范围是【 】
的取值范围是【 】
A、(−2, 6)
B、(−6, 2)
C、(−2, 4)
D、(−4, 6)
A
某中学的学生积极参加体育锻炼, 其中有 96% 的学生喜欢足球或游泳, 60% 的学生喜欢足球, 82% 的学生喜欢游泳, 则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是【 】
6 名同学到甲、乙、丙三个场馆做志愿者, 每名同学只去 1 个场馆, 甲场馆安排 1 名, 乙场馆安排 2 名, 丙场馆安排 3 名, 则不同的安排方法共有【 】
设集合 A = {x | 1 ⩽ x ⩽ 3}, B = {x | 2 < x < 4}, 则 A ∪ B =【 】
设数列 {an} 满足 a1 = 3, an+1 = 3an − 4n.(1) 计算 a2, a3, 猜想 {an} 的通项公式并加以证明;(2) 求数列 {2nan} 的前 n 项和 Sn.
已知向量=(2,5),=(λ,4),若//,则λ=_______.
已知a=(2,1),b=(2,-1),c=(0,1),则(a+b)·c=______;a·b=______.
已知λ>0,向量|a|=|b|=|c|=λ,且a∙b=0,c∙b=1,c∙a=2,则λ=________.
在∆ABC中,(CA)→=a,(CB)→=b,D是AC的中点,(CB)→=2(BE)→,试用a,b表示(DE)→=________;若(AB)→⊥DE→,求∠C的最大值为______.
如图已知点A(-12),B(3,4)若点P(m,0)使得 |PB|- |PA| 最大,则m的值为【 】
已知向量a ̅=(1,1),b ̅=(1,-1).若(a ̅+λb ̅)⊥(a ̅+μb ̅),则【 】
已知向量a→,b→满足|a→-b→ |=√3,|a→+b→ |=|2a→-b→|,则|b→ |=________.
已知向量a→,b→满足a→+b→=(2,3),a→-b→=(-2,1),则|a→ |²-|b→ |²=【 】
已知向量|a➝ |=1,|b➝ |=2,且a➝,b➝的夹角为120°.若a➝+tb➝与ta➝+b➝的夹角为锐角,则t的取值范围是__________.
i) 设直线ax+by+c=0,经过点(5,-4).求其系数a,b,c须满足的条件.ii)设直线ax+by+c=0,至原点之距离为 1,求其系数a,b,c须满足的条件.
已知一点 A(-1,-2),求至椭圆 x² + 5y² = 5 的切线方程.
已知一圆经过二圆 x²+y² -2x +3y -7=0及x²+y²+3y -4=0 的交点及点(-2,1),求其方程.
求与 x =0,y = 0,3x +4y - 6 = 0 三线相切之圆的方程
过点(0,-2)与圆x²+y²-4x-1=0相切的两条直线的夹角为α,则sinα=【 】
已知在△ABC中,A+B=3C,2 sin(A-C)=sinB.(1)求sinA;(2)设AB=5,求AB边上的高.
已知直线l:x-my+1=0与⨀C:(x-1)²+y²=4交于A,B两点,写出满足“△ABC的面积为8/5”的m的一个值______.
记△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为√3,D为BC的中点,且AD=1.(1)若∠ADC=π/3,求tanB;(2)若b²+c²=8,求b,c.