设i ̂,j ̂,k ̂分别为与三个坐标轴平行的单位向量,有向量a→=3i ̂+j ̂-k ̂,b→=i ̂+b2 j ̂+b3 k ̂,c→=c1 i ̂+c2 j ̂+c3 k ̂,其中,b2,b3,c1,c2,c3均为实数,且b2 b3>0,a→∙b→=0,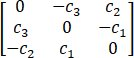
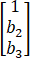 =
=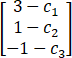 ,则下列叙述正确的有【 】
,则下列叙述正确的有【 】
A、a→∙c→=0
B、b→∙c→=0
C、|b→ |>√10
D、|c→ |≤√11
设i ̂,j ̂,k ̂分别为与三个坐标轴平行的单位向量,有向量a→=3i ̂+j ̂-k ̂,b→=i ̂+b2 j ̂+b3 k ̂,c→=c1 i ̂+c2 j ̂+c3 k ̂,其中,b2,b3,c1,c2,c3均为实数,且b2 b3>0,a→∙b→=0,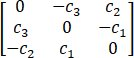
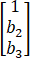 =
=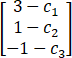 ,则下列叙述正确的有【 】
,则下列叙述正确的有【 】
A、a→∙c→=0
B、b→∙c→=0
C、|b→ |>√10
D、|c→ |≤√11
暂无答案
已知向量=(3,1),=(1,0),=+k,若⊥,则k=________.
若向量,满足||=3,| - |=5,∙=1,则||=________.
已知向量=(1,3),=(3,4),若(-λ)⊥,则λ=________.
已知向量=(2,5),=(λ,4),若//,则λ=_______.
已知a=(2,1),b=(2,-1),c=(0,1),则(a+b)·c=______;a·b=______.
如图,正方形ABCD的边长为3,则∙=__________.
在边长为1的等边三角形ABC中,D为线段BC上的动点,DE⊥AB且交AB于点E,DF//AB交AC于点F,则|2+|的值为__________;(+)∙最小值为__________.
已知平面向量,,(≠0)满足| |=1,| |=2,∙=0,(- )∙=0.记向量在,方向上的投影分别为x,y,-在方向的投影为z,则x2+y2+z2的最小值为________.
记△ABC的内角A,B,C的对边分别为a,b,c,已知b2=ac,点D在边AC上,BDsin∠ABC=asinC.(1)证明:BD=b;(2)若AD=2DC,求cos∠ABC.
在△ABC中,已知B=120°,AC=,AB=2,则BC=【 】
已知抛物线C:y2=2px(p>0)的焦点F到准线的距离为2.(1)求C的方程;(2)已知O为坐标原点,点P在C上,点Q满足=9,求直线OQ斜率的最大值.
双曲线x2/a2 -y2/b2 =1过点(,),离心率为2,则双曲线的解析式为【 】
已知抛物线C:y2=4x,焦点为F,点M在C上,且|FM|=6,则M的横坐标是______;作MN⊥x轴于N,则S△FMN=______.
已知二次函数y=x2﹣6x+5.(1)求出它的图象的顶点坐标和对称轴方程;(2)画出它的图象;(3)分别求出它的图象和x轴、y轴的交点坐标.
一条直线过点(1,-3),并且与直线2x+y-5=0平行,求这条直线的方程.
已知O为坐标原点,点A(1,1)在抛物线C:x2=2py(p>0)上,过点B(0,-1)的直线交C于P,Q两点,则【 】