在△ABC中,点D在边AB上,BD=2DA.记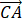 =m,
=m,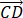 =n,则
=n,则 =【 】
=【 】
A、3m-2n
B、-2m+3n
C、3m+2n
D、2m+3n
在△ABC中,点D在边AB上,BD=2DA.记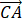 =m,
=m,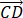 =n,则
=n,则 =【 】
=【 】
A、3m-2n
B、-2m+3n
C、3m+2n
D、2m+3n
B
【解析】
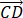 =2/3
=2/3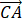 +1/3
+1/3  ⟹
⟹ =3
=3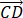 -2
-2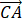 =3n-2m
=3n-2m
若集合M={x│√x<4},N={x│3x≥1},则M∩N=【 】
设f(x)=x2+a,记f1(x)=f(x),fn(x)=f(fn-1(x)),n=2,3,⋯,M={a∈R│对所有正整数n,|fn(0)|≤2}.证明:M=[-2,1/4].
给定整数n≥2,设M0 (x0,y0)是抛物线y2=nx-1与直线y=x的一个交点.试证明对任意正整数m,必存在整数k≥2,使(x0m,y0m)为抛物线y2=kx-1与直线y=x的一个交点.
袋内有8个白球和2个红球,每次从中随机取出一个球,然后放回一个白球,则第4次恰好取完所有红球的概率为________.
方程(x2006+1)(1+x2+x4+⋯+x2004 )=2006x2005的实数解的个数为__________.
已知椭圆x2/16+y2/4=1的左右焦点分别为F1与F2,点P在直线l:x-√3 y+8+2√3=0上.当∠F1 PF2取最大值时,比|PF1 |/(|PF2 |)的值为____________.
若对一切θ∈R,复数z=(a+cosθ)+(2a-sinθ)i的模不超过2,则实数a的取值范围为__________________.
已知向量=(-1,2),=(3,m),若⊥,则m=________.
若向量a=(1,1),b=(1,-1),c=(-1,2),则c=【 】
已知向量a ̅=(1,1),b ̅=(1,-1).若(a ̅+λb ̅)⊥(a ̅+μb ̅),则【 】
已知向量a→,b→满足|a→-b→ |=√3,|a→+b→ |=|2a→-b→|,则|b→ |=________.
已知向量a→,b→满足a→+b→=(2,3),a→-b→=(-2,1),则|a→ |²-|b→ |²=【 】
已知向量|a➝ |=1,|b➝ |=2,且a➝,b➝的夹角为120°.若a➝+tb➝与ta➝+b➝的夹角为锐角,则t的取值范围是__________.