如图所示,在锐角△ABC中,AB>AC,H是垂心,AM是中线,BE⊥AC于点E,CF⊥AB于F.点D在BC边上,满足∠CAD=∠BAM且∠ADH=∠MAH,证明:EF平分线段AD.
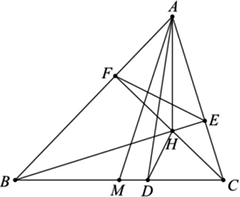
如图所示,在锐角△ABC中,AB>AC,H是垂心,AM是中线,BE⊥AC于点E,CF⊥AB于F.点D在BC边上,满足∠CAD=∠BAM且∠ADH=∠MAH,证明:EF平分线段AD.

记△ABC,△HBC的外接圆分别为圆O,圆P,由三角形垂心性质知,圆O、圆P关于点M对称.设AM的延长线与圆P相交于点N,连接HN,BN,CN,则AM=MN.从而四边形ABNC为平行四边形因此BN⊥BE,点P在HN上.又OP//AH且OP=AH, 所以HP//AO,即HN//AO. 易知∠BAO=∠CAH又∠BAM=∠CAD,所以∠OAM=∠HAD从而∠ADH=∠MAH=∠DAO,因此HD//OA,即点D在HN上.设AD的延长线与圆O相交于点G,则AD•DG=BD•DC=HD•DN,所以A、N、G、H四点共圆.因此∠AGH=∠ANH=∠OAM=∠GAH,又OA=OG,所以AD⊥OH.设AD、EF相交于点T,直线EF、BC相交于点K,由题设知B、C、E、 F四点共圆。所以∠BAO=90°-∠...
查看完整答案如图,∠ABC=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是D,E.已知AD=8,BE=3,则DE=______.
已知△ABC三内角的大小成等差数列,tanAtanC=2+,求角A,B,C的大小;又知顶点C的对边c上的高等于4,求三角形各边a,b,c的长.(提示:必要时可验证(1+)2=4+2)
CD为直角三角形ABC中斜边AB上的高,已知△ADC,△CBD,△ABC的面积成等比数列,求∠B(用反三角函数表示).
在△ABC的边AB,AC上各取D,E点,使AD=1/3 AB,AE=1/3 AC,连结BE,CD相交于F点.求证:S△FBC=1/2 S△ABC.