高中数学-高考试题(全国统考 1980年三角形)

问答题（1980年全国统考）

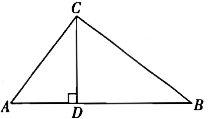
CD为直角三角形ABC中斜边AB上的高，已知△ADC,△CBD,△ABC的面积成等比数列，求∠B(用反三角函数表示).

答案解析

由题设有(CD∙BD)2=(CD∙AD)∙(CD∙AB)∴ BD2=AD∙AB但 AC2=AD∙AB∴ BD=AC.由 tanB=CD/BD,cosB=sinA=CD/AC=CD/BD,∴ tanB=C...

查看完整答案

讨论

高中数学

设三角函数f(x)=sin⁡(kx/5+π/3)，其中k≠0.(Ⅰ) 写出f(x)的极大值M 、极小值 m 与最小正周期T; (Ⅱ) 试求最小的正整数k，使得当自变量 x 在任意两个整数间（包括整数本身）变化时，函数f(x)至少有一个值是 M 与一个值是 m .

直升飞机上一点 P 在地平面 M 上的正射影是 A ．从P看地平面上一物体 B （不同于 A ) ，直线P B 垂直于飞机窗玻璃所在的平面 N（如图）．证明：平面 N 必与平面 M 相交，且交线 l 垂直于 AB.

证明对数换底公式：logbN=logaN/logab.(a,b,N都是正数，a≠1,b≠1)

用解析几何方法证明三角形的三条高线交于一点.

半径为 1 , 2 , 3 的三个圆两两外切．证明：以这三个圆的圆心为顶点的三角形是直角三角形．

将多项式x5y-9xy5分别在下列范围内分解因式：1. 有理数范围； 2. 实数范围；3. 复数范围．

设等腰△OAB的顶角为 2θ，高为h.(1) 在△OAB内有一动点P，到三边OA,OB,AB的距离分别为|PD|,|PF|,|PE|，并且满足关系式|PD|∙|PF|=|PE|2，求P点的轨迹.(2) 在上述轨迹中定出点P的坐标，使得|PD|+|PE|=|PF|.

试问数列：lg100,lg⁡(100sinπ/4),lg⁡(100sin2π/4),⋯,lg⁡(100sinn-1π/4)，前多少项的和的值最大？并求出这大值（这里取lg2=0.301）

设 CEDF 是一个已知圆的内接矩形，过 D 作该圆的切线与 CE 的延长线相交于点 A ，与 CF 的延长线相交于点 B . 求证：BF/AE=BC3/AC3 .

美国的物价从 1939 年的 100 增到四十年后 1979年的 500 ，如果每年物价增长率相同，问每年增长百分之几？（注意：自然对数 Inx 是以 e = 2.718 … 为底的对数．本题中增长率 x < 0.1，可用自然对数的近似公式：ln(1+x)≈x，取lg2=0.3 , In10=2.3 来计算．)

三角形

试证: 直角三角形之弦上正方形之面积，与其他两边之平方形面积之和相等.

证明 △ABC 中过 B,C 二顶点之二中线等长，则 △ABC 为等腰，并证明其逆定理.

试证三角形之高为垂足所成三角形之各角的角二等分线.

三角形内任意一点至三顶点 A,B,C 的延长线交对边于 P,Q,R，则BP/CP×CQ/AQ×AR/BR=1.

已知底边顶角及底边上之高,求作一三角形.

设 ABC 为一直角三角形，A 为直角，A 之平分线与 BC 交于 D，与此三角形之外接圆交于 B.求证: △ABC 之面积 =1/2 AD×AE.

对于已知圆，作一外接三角形，与已知三角形相似.

等积各三角形，证明其等腰者周界为极小，当其底相等时.

三角形ABC中，自A、B两点各作对边垂线，垂足为D、E，设M、N为DE及AB之两中点，证明MN⊥DE.

三角形ABC中，其边为a,b,c，内接圆半径为r，试证：a+b+c=2r(cot⁡(A/2)+cot(B/2)+cot(C/2))

平面几何

求内接于圆之正六角形与外切正三角形之面积之比.

两圆相外切 (tangent externally) 于 A，又有一外公切线 (common external tangent) 切两圆于 B 及 C，试证 ∠BAC 为直角(right angle).

已知三角形之三角及其面积，求作其圆.

何谓圆：___________________________.

作直线垂直于一已知线，与已知圆相切.

设G为半径为R的圆，G1,G2,⋯,Gn为半径为r的圆，已知G1,G2,⋯,Gn均外切于G，对于i=1,2,⋯,n-1，Gi与Gi+1外切，且Gn与G1外切，则下列叙述正确的有【】

从半圆之直径 AB 两端各引此半圆弦 AC,BD交于 E，求证: AC·AE+BD·BE = AB².

两圆外切，其半径各为R和r，设两圆之外公切线之交角为θ，试证 sinθ=.

于圆内接四边形内，若两对角线成垂直，求证对角线交点与一边中点之距离等于自圆心至对边之距离.

于三角形 ABC之BC边上任取X点作ABX及ACX两圆.(1)求证此两圆直径之比为AB:AC；(2)若BX:XC=m:n,试示①(m+n)cotAXC=ncotB-mcotC.②(m+n)2 AX2=(m+n)(mb2+nc2 )-mna2，其中a=BC,b=CA,c=AB.