-
关注“优题吧”，分配平台账号.
竞赛2024年东南地区奥林匹克( )
如图，在△ABC中，AB>AC,△ABC的内切圆I分别切边BC,CA,AB于点D,E,F.设M为DE的中点，N为DF的中点，直线EF与BC相交于点P，过点P作动直线l交内切圆I于不同的两点G,H,且I,M,G和I,N,H均不共线，△IMG的外接圆与△INH的外接圆交于不同于I的点Q,证明：点Q始终在一个定圆上.
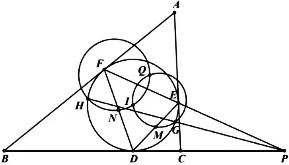
解答过程见word版
竞赛2024年东南地区奥林匹克( )
求最大的正整数n，使得平面上存在n个点P1,P2,⋯,Pn(任意三点不共线)和不过其中任意点的n条直线l1,l2,⋯,ln(任意三线不共点)，满足对任意i≠j，直线Pi Pj,li,lj三线共点.
当n=3时，任取不共线的三点P1,P2,P3，在P1 P2,P2 P3,P3 P1上各取非端点的一点Q1,Q2,Q3，取l1,l2,l3分别为直线Q1 Q2,Q2 Q3,Q3 Q1即可.
当n=4时，设对于{i,j}≠{3,4}均有li,lj,Pi Pj共点于Aij，并记直线l3,l4交于点A34，再设P1 A34,l2交于X,P2 A34,l1交于Y(这里X,Y可以是无穷远点).
由于Aij在li上，故Aij≠Pi.若Pi在li (i≠j)上，则由Pi,Pj,Aij共线推出Pj在lj上，矛盾.
对六边形A12 A13 P1 A34 P2 A23应用帕普斯定理得X,Y,P3共线；
对六边形A12 A14 P1 P34 P2 A24应用帕普斯定理得X,Y,P4共线.
从而X,Y,P3,P4四点共线，若A34也在该线上会导致P1也在该线上，于是P1,P3,P4共线，矛盾.
从而n=4时不满足条件，显然可得n>4也不满足条件.
综上，满足条件的最大正整数为n=3.
竞赛2024年东南地区奥林匹克( )
在锐角三角形△ABC中，AB>AC,O为外心. 设D为BC上一点，O1,O2分别为△ABD,△ACD的外心，△AO1O2的外接圆与⨀O交于不同于A的点L.
证明：A,O,D三点共线当且仅当AL//BC.
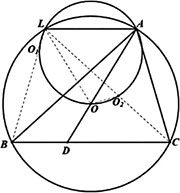
由萨蒙定理知A,O1,O,O2四点共圆.
事实上，∠AO1 O=1/2∠AO1 B=∠ADC,
同理可得∠AO2 O=∠ADB，
∴∠AO1 O+∠AO2 O=180°.
设BO1∩CO2=L，则∠ABO1=90°-∠ADC=∠ACO2，
∴A,C,B,L四点共圆，即L在⨀O上,
∴∠ALO2=∠ABC=∠AOO2，
∴A,L,O,O1,O2五点共圆.
∵AB>AC，于是
A,O,D三点共线⟺∠ADC=∠B+90°-∠C
⟺∠O2 CA=90°-∠ADC=90°-(∠B+90°-∠C)=∠C-∠B
⟺∠BCL=∠B
⟺AC=LB
⟺AL//BC.
竞赛2024年东南地区奥林匹克( )
在n×n的方格表中，若两个方格有公共边，则称它们是相邻的.若l个互异方格A1,A2,⋯,A_l满足Ai和Ai+1相邻（1≤i≤l-1），则称它们为一条长度为l的“龙”.求最大正整数k，使得可以给每个方格填上0或者1，并且对任意一个方格A，和以A中数字为首项的0,1序列m1,m2,⋯,mk，都存在从A开始的长度为k的龙，方格中的数字依次是m1,m2,⋯,mk.
解答过程见word版
竞赛2024年东南地区奥林匹克( )
设P为平面凸多边形，若线段AB的两端点在P的边界上，并且过A,B与AB垂直的两条直线之间的区域(含边界)包含P，则称线段AB为“锦弦”. 求最大的正整数k，使得任意平面凸多边形P都有k条锦弦.
解答过程见word版