如图,在△ABC中,AB>AC,△ABC的内切圆I分别切边BC,CA,AB于点D,E,F.设M为DE的中点,N为DF的中点,直线EF与BC相交于点P,过点P作动直线l交内切圆I于不同的两点G,H,且I,M,G和I,N,H均不共线,△IMG的外接圆与△INH的外接圆交于不同于I的点Q,证明:点Q始终在一个定圆上.
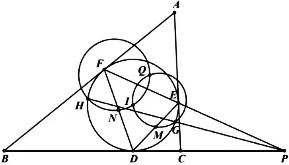
如图,在△ABC中,AB>AC,△ABC的内切圆I分别切边BC,CA,AB于点D,E,F.设M为DE的中点,N为DF的中点,直线EF与BC相交于点P,过点P作动直线l交内切圆I于不同的两点G,H,且I,M,G和I,N,H均不共线,△IMG的外接圆与△INH的外接圆交于不同于I的点Q,证明:点Q始终在一个定圆上.

解答过程见word版
在锐角三角形△ABC中,AB>AC,O为外心. 设D为BC上一点,O1,O2分别为△ABD,△ACD的外心,△AO1O2的外接圆与⨀O交于不同于A的点L.证明:A,O,D三点共线当且仅当AL//BC.
已知:如图,MN为圆的直径,P、C为圆上两点,连PM、PN,过C作MN的垂线与MN、MP和NP的延长线依次相交于A、B、D,求证:AC2=AB·AD.
如图所示,O是△ABC的内心,∠BOC=100°,则∠BAC=______度.
过四点(0,0),(4,0),(-1,1),(4,2)中的三点的一个圆的方程为____________.
如图所示,四边形ABCD内接于圆,(AB) ̅=5,(AC) ̅=3√5,(AD) ̅=7,∠BAC=∠CAD,则圆的半径为【 】
设P为平面凸多边形,若线段AB的两端点在P的边界上,并且过A,B与AB垂直的两条直线之间的区域(含边界)包含P,则称线段AB为“锦弦”. 求最大的正整数k,使得任意平面凸多边形P都有k条锦弦.
求最大的正整数n,使得平面上存在n个点P1,P2,⋯,Pn(任意三点不共线)和不过其中任意点的n条直线l1,l2,⋯,ln(任意三线不共点),满足对任意i≠j,直线Pi Pj,li,lj三线共点.
在△ABC中,AB=1,AC=3,∠BAC=π/2,半径为r>0的圆与边AB,AC相切,且也内切于△ABC的外接圆,则r的值为__________.
设由圆外一点作一切线一割线,证明此切线为割线及其圆外线分的比例中率.
设一圆之半径为 25 尺,其外切四边形之圆界为 400 尺,试求此四边形之面积。