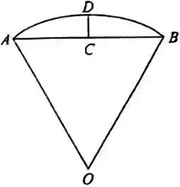
沈括的《梦溪笔谈》是中国古代科技史上的杰作，其中收录了计算圆弧长度的“会圆术”.如图，(AB) ̂是以O为圆心，OA为半径的圆弧，C是AB的中点，D在(AB) ̂上，CD⊥AB.“会圆术”给出(AB) ̂的弧长的近似值s的计算公式：s=AB+CD2/OA.当OA=2,∠AOB=60°时，s=【 】
A、 (11-3√3)/2
B、(11-4√3)/2
C、(9-3√3)/2
D、(9-4√3)/2
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
单项选择（2022年全国甲·理）
答案解析
B连接OC，∵C是AB的中点，∴OC⊥AB，又CD⊥AB，∴O,C,D三点共线，即OD=OA=OB=2，又∠AOB=60°，∴AB=OA=OB=2，∴OC=√3,CD=2-√3,∴s=AB+(CD^2...
查看完整答案讨论
在长方体ABCD-A1B1C1D1中，已知B1D与平面ABCD和平面AA1B1B所成的角均为30°，则【 】
当x=1时，函数f(x)=a lnx+b/x取得最大值-2，则f'(2)=【 】
函数y=(3x-3-x) cosx在区间[-π/2,π/2]的图像大致为【 】
如图，网格纸上绘制的是一个多面体的三视图，网格小正方形的边长为1，则该多面体的体积为【 】
设全集U={-2,-1,0,1,2,3}，集合A={-1,2},B={x∣x2-4x+3=0}，则∁U(A∪B)=【 】
从分别写有1，2，3，4，5，6的6张卡片中无放回随机抽取2张，则抽到的2张卡片上的数字之积是4的倍数的概率为【 】
已知函数f(x)=xeax-ex．（1）当a=1时，讨论f(x)的单调性；（2）当x>0时，f(x)<-1，求a的取值范围；（3）设n∈N^*，证明：1/+1/+⋯+1/>ln( n+1)．
于圆内接四边形内，若两对角线成垂直，求证对角线交点与一边中点之距离等于自圆心至对边之距离.
证明：对于一组共轴圆 (co-axial circles) 一定点之诸极线 (polars) 必通过一定点，且一定直线之诸极 (poles) 必在一直线上.
设R为三角形之外接圆半径，试证 acosA+bcosB+ccosC = 4RsinAsinBsinC.
AO 为圆之半径，过垂直于此之直径上一点 B，引任意弦 BP，从此弦之一端P 引切线 PC 与OB 之延线会于 C，证 CB =CP.
设二圆之连心线交一圆于 A,B 两点，交第二圆于 D,C 二点，又交二圆之一外公切线于 P 点，设在连心线上，点 A 距 P 最近，点 D 距 P 最远，试证：PA· PD = PB·PC.
圆内接四边形 ABCD 内，∠A = 90°,AB = a,BC = b，其面积为 c²，求CD,DA 及圆半径之长.
为了测湖岸边A、B两点的距离，选择一点C，测得CA=50米，CB=30米，∠ACB=120°，求AB.
已知D为△ABC内的一点，AB=AC=1，∠BAC=63°，∠BAD=33°，∠ABD=27°，求DC(精确到小数点后两位，sin27°=0.4540).
如图，在三角形ABC中∠BAC=60°，BD平分∠ABC，交AC于D，CE平分∠ACB交AB于E，BD和CE交于F，则∠EFB=【 】
若三角形的两边不等，它的对不等边的两角也必不等，并且大角必对大边.
△ABC 之边 AC 之三等分点之中，设近于 A 之点为 D，而 BC 之中点为 E时，则 AE 为 BD 所二等分.
证明 △ABC 中过 B,C 二顶点之二中线等长，则 △ABC 为等腰，并证明其逆定理.
三角形内任意一点至三顶点 A,B,C 的延长线交对边于 P,Q,R，则BP/CP×CQ/AQ×AR/BR=1.
设 D 为 △ABC 之底边 BC 之中点，若顶角 A 为角直角或锐角，则底边BC 分别大于，等于或小于中线 AD 之二倍.试证之.