如图,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为1,则该多面体的体积为【 】
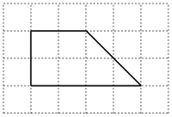


A、8
B、12
C、16
D、20
如图,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为1,则该多面体的体积为【 】



A、8
B、12
C、16
D、20
B
【解析】
由三视图还原几何体,如图,

则该直四棱柱的体积V=(2+4)/2×2×2=12.
设全集U={-2,-1,0,1,2,3},集合A={-1,2},B={x∣x2-4x+3=0},则∁U(A∪B)=【 】
从分别写有1,2,3,4,5,6的6张卡片中无放回随机抽取2张,则抽到的2张卡片上的数字之积是4的倍数的概率为【 】
已知函数f(x)=xeax-ex.(1)当a=1时,讨论f(x)的单调性;(2)当x>0时,f(x)<-1,求a的取值范围;(3)设n∈N^*,证明:1/+1/+⋯+1/>ln( n+1).
如图,PO是三棱锥P-ABC的高,PA=PB,AB⊥AC,E是PB的中点.(1)求证:OE//平面PAC;(2)若∠ABO=∠CBO=30°,PO=3,PA=5,求二面角C-AE-B的正弦值.
已知{an }为等差数列,{bn}是公比为2的等比数列,且a2-b2=a3-b3=b4-a4.(1)证明:a1=b1;(2)求集合{ k| bk=am+a1,1≤m≤500}中元素个数.
已知正三棱台上底面边长为2,下底面边长为4,且侧棱与底面所成的角是45°,那么这个正三棱台的体积等于__________.
已知圆台的上、下底面半径分别为r,2r,侧面积等于上、下底面积之和,则圆台的高为_______.
在体积为V的斜三棱柱ABC-A'B'C'中,已知S是侧棱CC'上的一点,过点S,A,B的截面截得的三棱锥的体积为V1,那么过点S,A',B'的截面截得的三棱锥的体积为______.
如图,已知:在直三棱柱ABC-A1B1C1中,∠ACB = 90°,∠BAC=30°,BC=1,AA1= ,M是 CC1 的中点.求证AB1⊥A1M.
已知轴截面是正方形的圆柱的高与球的直径相等,则圆柱的全面积与球的表面积的比是【 】
长方体的全面积为11,12条棱长度之和为24,则这个长方体的一条对角线长为【 】
在半径为30m的圆形广场中央上空,设置一个照明光源,射向地面的光呈圆锥形,且其轴截面顶角为120°。若要光源恰好照亮整个广场,则其高度应为________(精确到0.1m)。
建造一个容积为8m3,深为2m的长方体无盖水池。如果池底和池壁的造价每平方米分别为120元和80元,那么水池的最低总造价为________元。
如图是一个多面体的三视图, 这个多面体某条棱的一个端点在正视图中对应的点为 M, 在俯视图中对应的 点为 N, 则该端点在侧视图中对应的点为【 】
如图,E,F分别为正方形的面ADD1A1、面BCC1B1的中心,则四边形在该正方形BFD1E的面上的射影可能是________.(要求:把可能的图的序号都填上)
某几何体的三视图 (单位: cm) 如图所示, 则该几何体的体积 (单位: cm3) 是【 】
某三棱柱的底面为正三角形, 其三视图如图所示, 该三棱柱的表面积为【 】
在一个正方体中,过顶点A的三条棱的中点分别为E,F,G,该正方体截去三棱锥A-EFG后,所得多面体的三视图中,正视图如右图所示,则相应的侧视图是【 】
以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某三棱锥的三视图,则所选侧视图和俯视图的编号依次为______ ( 写出符合要求的一组答案即可).