高中数学-高考试题(新高考Ⅱ 2022年统计图表)

问答题（2022年新高考Ⅱ）

在某地区进行流行病调查，随机调查了100名某种疾病患者的年龄，得到如下的样本数据频率分布直方图．

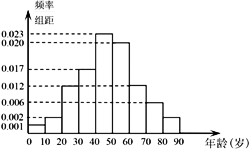
（1）估计该地区这种疾病患者的平均年龄（同一组中的数据用该组区间的中点值作代表）；

（2）估计该地区一人患这种疾病年龄在区间[20,70)的概率；

（3）已知该地区这种疾病的患病率为0.1%，该地区年龄位于区间[40,50)的人口占该地区总人口的16%，从该地区任选一人，若此人年龄位于区间[40,50)，求此人患该种疾病的概率．（样本数据中的患者年龄位于各区间的频率作为患者年龄位于该区间的概率，精确到0.0001）.

答案解析

（1）平均年龄x ̅=(5×0.001+15×0.002+25×0.012+35×0.017+45×0.023 +55×0.020+65×0.012+75×0.006+85×0.002)×10=44.65（岁）．（2）设A={一人患这种疾病的年龄在区间[20,70) }，所以P(A)=1-P(A ̅ )=1-(0.00...

查看完整答案

讨论

统计

据报道,我国目前已成为世界上受荒漠化危害最严重的国家之一.左下图表示我国土地沙化总面积在20世纪五六十年代、七八十年代、九十年代的变化情况.由图中的相关信息，可将上述有关年代中,我国年平均土地沙化面积在右下图中图示为:

从某网络平台推荐的影视作品中抽取400部，统计其平分数据，将所得400个评分数据分为8组：[60,70],[70,74],…,[94,98]，并整理得到如下的频率分布直方图，则评分在区间[82.86)内的影视作品数量为【】

某校一个课外学习小组为研究某作物种子的发芽率 y 和温度 x (单位: °C) 的关系, 在 20 个不同的温度条件下进行种子发芽实验, 由实验数据 (xi, yi) (i = 1, 2, · · · , 20) 得到下面的散点图:由此散点图, 在 10°C 至 40°C 之间, 下面四个回归方程类型中最适宜作为发芽率 y 和温度 x 的回归方程类型的是【】。

某厂接受了一项加工业务, 加工出来的产品 (单位: 件) 按标准分为 A, B, C, D 四个等级. 加工业务约定: 对于A 级品、 B 级品、 C 级品, 厂家每件分别收取加工费 90 元, 50 元, 20 元; 对于 D 级品, 厂家每件要赔偿原料损失费 50 元. 该厂有甲、乙两个分厂可承接加工业务. 甲分厂加工成本费为 25 元/件, 乙分厂加工成本费为 20 元/件.厂家为决定由哪个分厂承接加工业务, 在两个分厂各试加工了 100 件这种产品, 并统计了这些产品的等级, 整理如下:(1) 分别估计甲、乙两分厂加工出来的一件产品为 A 级品的概率;(2) 分别求甲、乙两分厂加工出来的 100 件产品的平均利润, 以平均利润为依据, 厂家应选哪个分厂承接加工业务?

某学生兴趣小组随机调查了某市 100 天中每天的空气质量等级和当天到公园锻炼的人次, 整理数据得到下表 (单位: 天):(1) 分别估计该市一天的空气质量等级为 1, 2, 3, 4 的概率;(2) 求一天中到该公园锻炼的平均人次的估计值 (同一组中的数据用改组区间的中点值为代表);(3) 若某天的空气质量等级为 1 或 2, 则称这天“空气质量好” ; 若某天的空气质量等级为 3 或 4, 则称这天“空气质量不好” . 根据所给数据, 完成下列的 2 × 2 列联表, 并根据列联表, 判断是否有 95% 的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?

为加强环境保护, 治理空气污染, 环境监测部门对某市空气质量进行调研, 随机抽查了 100 天空气中的 PM2.5和SO2 浓度 (单位: ug/m3), 得下表:(1) 估计事件“该市一天空气中 PM2.5 浓度不超过 75, 且SO2 浓度不超过 150”的概率;(2) 根据所给数据, 完成下面的 2 × 2 列联表:(3) 根据 (2) 中的列联表, 判断是否有 99% 的把握认为该市一天空气中 PM2.5 浓度与SO2 浓度有关?附：

从一批零件中抽取 80 个, 测量其直径 (单位: mm), 将所得数据分为 9 组: [5.31, 5.33], [5.33, 5.35], · · · ,[5.45, 5.47], [5.47, 5.49], 并整理得到如下频率分布直方图, 则在被抽取的零件中, 直径落在区间 [5.43, 5.47] 内的个数为【】

某沙漠地区经过治理, 生态系统得到很大改善, 野生动物数量有所增加, 为调查该地区某种野生动物的数量,将其分成面积相近的 200 个地块, 从这些地块中用简单随机抽样的方法抽取 20 个作为样区, 调查得到样本数据(xi,yi) (i=1,2,…,20), 其中 xi 和 yi 分别表示第 i 个样区的植物覆盖面积 (单位: 公顷) 和这种野生动物的数量,并计算得=60, =1200, =80, =9000, = 800.(1) 求该地区这种野生动物数量的估计值 (这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数) ;(2) 求样本 (xi, yi) (i = 1, 2, … , 20) 的相关系数 (精确到 0.01) ;(3) 根据现有统计资料, 各地块间植物覆盖面积差异很大, 为提高样本的代表性以获得该地区这种野生动物数量更准确的估计, 请给出一种你认为更合理的抽样方法, 并说明理由.附: 相关系数 r = , ≈ 1.414.

为满足人民对美好生活的向往, 环保部门要求相关企业加强污水治理, 排放未达标的企业要限期整改. 设企业的污水排放量 W 与时间 t 的关系为 W = f(t). 用 -(f(b)-f(a))/(b-a)的大小评价在 [a, b] 这段时间内企业污水治理能力的强弱. 已知整改期内, 甲、乙两企业的污水排放量与时间的关系如下图所示.① 在 [t1, t2] 这段时间内, 甲企业的污水治理能力比乙企业强;② 在 t2 时刻, 甲企业的污水治理能力比乙企业强;③ 在 t3 时刻, 甲、乙两企业的污水排放都已达标;④ 甲企业在 [0, t1], [t1, t2], [t2, t3] 这三段时间中, 在 [0, t1] 的污水治理能力最强.其中所有正确结论的序号是__________.

已知 1, 2, a, b 的中位数是 3, 平均数是 4, 则 ab =______.

几何概型

设O为正方形 ABCD 的中心, 在 O,A,B,C,D 中任取 3 点, 则取到的 3 点共线的概率为【】

在区间(0,1)与(1,2)中各随机取1个数，则两数之和大于7/4的概率为【】

在区间(0,1/2]随机取1个数，则取到的数小于1/3的概率为【】

袋内有8个白球和2个红球，每次从中随机取出一个球，然后放回一个白球，则第4次恰好取完所有红球的概率为________.

甲乙两人投篮, 每次由其中一人投篮，规则如下：若命中则此人继续投篮，若未命中则换为对方投篮. 无论之前投篮情况如何, 甲每次投篮的命中率均为 0.6，乙每次投篮的命中率均为0.8，由抽签决定第一次投篮的人选，第一次投篮的人是甲、乙的概率各为0.5.(1)求第2次投篮的人是乙的概率；(2)求第i次投篮的人是甲的概率；(3)已知：若随机变量X_i服从两点分布，且P(Xi=1)=1-P(Xi=0)=qi,i=1,2,⋯,n，则E(Xi )=qi ，记前n次（即从第1次到第n次投篮）中甲投篮的次数为Y，求E(Y).

为研究某种农产品价格变化的规律，收集得到了该农产品连续40天的价格变化数据,如下表所示.在描述价格变化时,用“+”表示“上涨”,即当天价格比前一天价格高；用“-”表示“下跌”，即当天价格比前一天价格低；用“0”表示“不变”，即当天价格与前一天价格相同.时段价格变化第1天到第20天 - + + 0 - - - + + 0 + 0 - - + - + 0 0 +第21天到第40天 0 + + 0 - - - + + 0 + 0 + - - - + 0 - +用频率估计概率.(1)试估计该农产品价格“上涨”的概率；(2)假设该农产品每天的价格变化是相互独立的，在未来的日子里任取4天，试估计该农产品价格在这4天中2天“上涨”、1天“下跌”、1天“不变”的概；(3)假设该农产品每天的价格变化只受前一天价格变化的影响，判断第41天该农产品价格“上涨”“下跌”和“不变”的概率估计值哪个最大(结论不要求证明).

在矩形ABCD中，AD=2AB，E，F分别为AD，BC的中点，从A、B、C、D、E、F中任选三个点，则这三个点为顶点可组成的直角三角形的概率【】

在一项传染病研究中，收集了900位患者的样本，发现其中：190人有发热症状，220人有咳嗽症状，220人有呼吸困难症状，330人发热或咳嗽，350人咳嗽或呼吸困难，340人发热或呼吸困难，30人同时出现发热、咳嗽、呼吸困难的症状。从这900人中随机抽取一人，则至少出现一种症状的概率是__________.

甲有两张牌a,b，乙有x,y，甲乙各任取一张牌，则甲取出牌不小于乙取出牌的概率不小于1/2.【】(1)a > x.(2)a+b>x+y·

甲能解某题之几率为b/a，乙能解某题之几率为d/c，设甲与乙独自解之，试用两种方法,求某题能解之几率.

统计图表

为了解某地农村经济情况，对该地农户家庭年收入进行抽样调查，将农户家庭年收入的调查数据整理得到如下频率分布直方图:根据此频率分布直方图，下面结论中不正确的是【】

甲、乙两台机床生产同种产品，产品按质量分为一级品和二级品,为了比较两台机床产品的质量，分别用两台机床各生产了200件产品，产品的质量情况统计如下表：(1)甲机床、乙机床生产的产品中一级品的频率分别是多少？(2)能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异？附：K2=，

分别统计了甲、乙两位同学16周的各周课外体育运动时长（单位：h），得如下茎叶图：则下列结论中错误的是【】

为研究某药品的疗效，选取若干名志愿者进行临床试验，所有志愿者的舒张压数据(单位：kPa)的分组区间为[12,13)，[13,14)，[14,15)，[15,16)，[16,17]，将其按从左到右的顺序分别编号为第一组，第二组，，第五组，下图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人，第三组中没有疗效的有6人，则第三组中有疗效的人数为【】

某社区通过公益讲座以普及社区居民的垃圾分类知识．为了解讲座效果，随机抽取10位社区居民，让他们在讲座前和讲座后各回答一份垃圾分类知识问卷，这10位社区居民在讲座前和讲座后问卷答题的正确率如下图：则【】

执行如图的程序框图, 若输入 k = 0, a = 0, 则输出的 k 为【】

已知 C1, C2 的参数方程分别为 C1 :(θ为参数)， C2 : (t 为参数) ,(1) 将 C1, C2 的参数方程化为普通方程;(2) 以坐标原点为极点, x 轴正半轴为极轴建立极坐标系, 设 C1, C2 的交点为 P , 求圆心在极轴上, 且经过极点和 P 的圆的极坐标方程.

正三棱台高为1，上下底边长分别为3√3和4√3，所有顶点在同一球面上，则球的表面积是【】

如图，四边形ABCD为正方形， ED⊥平面ABCD，FB//ED,AB=ED=2FB，记三棱锥E-ACD,F-ABC，F-ACE的体积分别为V1,V2,V3，则【】

如图是一个多面体的三视图, 这个多面体某条棱的一个端点在正视图中对应的点为 M, 在俯视图中对应的点为 N, 则该端点在侧视图中对应的点为【】