高考2024年天津市( )
下列图中,相关性系数最大的是【 】
A、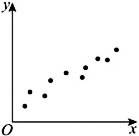
B、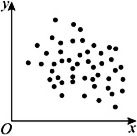
C、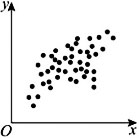
D、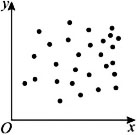

观察4幅图可知,A图散点分布比较集中,且大体接近某一条直线,线性回归模型拟合效果比较好,呈现明显的正相关,|r|值相比于其他3图更接近1.
高考2024年上海市( )
为了解某地初中学生体育锻炼时长与学业成绩的关系,从该地区29000名学生中抽取580人,得到日均体育锻炼时长与学业成绩的数据如下表所示:
时间范围学业成绩 [0,0.5) [0.5,1) [1,1.5) [1.5,2) [2,2.5)
优秀 5 44 42 3 1
不优秀 134 147 137 40 27
(1)该地区 29000名学生中体育锻炼时长不少于1小时人数约为多少?
(2)估计该地区初中学生日均体育锻炼的时长(精确到0.1);
(3)是否有95%的把握认为学业成绩优秀与日均体育锻炼时长不小于1小时且小于2小时有关?(附:χ²=n(ad-bc)²/((a+b)(c+d)(a+c)(b+d)),其中n=a+b+c+d,P(χ²≥3.841)≈0.05)
解答过程见word版
高考2024年北京市( )
已知某险种的保费为0.4万元,前3次出险每次赔付0.8万元,第4次赔付0.6万元
在总体中抽样 100单,以频率估计概率:
赔偿次数 0 1 2 3 4
单数 800 100 60 30 10
(1)求随机抽取一单,赔偿不少于2次的概率;
(2)(i)毛利润是保费与赔偿金额之差。设毛利润为X,估计X的数学期望;
(ii)若未赔偿过的保单下一保险期的保费下降4%,已赔偿过的增加20%. 估计保单下一保险期毛利润的数学期望.
解答过程见word版
高考2024年全国甲·理( )
某工厂进行生产线智能化升级改造,升级改造后,从该工厂甲、乙两个车间的产品中随机抽取150件进行检验,数据如下:
优级品 合格品 不合格品 总计
甲车间 26 24 0 50
乙车间 70 28 2 100
总计 96 52 2 150
(1)填写如下列联表:
优级品 品优级品
甲车间
乙车间
能否有95%的把握认为甲乙两车间产品的优级品率存在差异?能否有99%的把握认为甲、乙两车间产品的优级品率存在差异?
(2)已知升级改造前该工厂产品的优级品率p=0.5.设p ̅为升级改造后抽取的n件产品的优级率.如果p ̅>p+1.65√((p(1-p))/n),则认为该工厂产品的优级品率提高了.根据抽取的150件产品率.能否认为生产线智能化升级改造后,该工厂产品的优级品率提高了?( √150≈12.247)
附:K²=n(ad-bc)²/((a+b)(c+d)(a+c)(b+d))
P(K²≥k) 0.050 0.010 0.001
k 3.841 6.635 10.828
解答过程见word版
高考2024年新高考Ⅱ( )
某农业研究部门在面积相等的 100 块稻田上种一种新型水稻,得到各块的亩产量(单位:kg)并部分整理为下表:
亩产量 (900,950) (950,1000) (1000,1050) (1100,1150) (1150,1200)
频数 6 12 18 24 10
据表中数据,结论正确的是【 】
A、100 块稻田亩产量的中位数小于1050kg
B、100 块稻中亩产量低于 1100kg 的稻田所占比例超过 80%
C、100 块稻亩产量的极差介于 200kg 至300kg 之间
D、100 块稻田亩产量的平均值介于 900kg 至 1000kg 之间
解答过程见word版

