已知函数f(x)=xeax-ex.
(1)当a=1时,讨论f(x)的单调性;
(2)当x>0时,f(x)<-1,求a的取值范围;
(3)设n∈N^*,证明:1/ +1/
+1/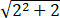 +⋯+1/
+⋯+1/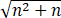 >ln( n+1).
>ln( n+1).
已知函数f(x)=xeax-ex.
(1)当a=1时,讨论f(x)的单调性;
(2)当x>0时,f(x)<-1,求a的取值范围;
(3)设n∈N^*,证明:1/ +1/
+1/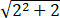 +⋯+1/
+⋯+1/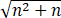 >ln( n+1).
>ln( n+1).
(1)当a=1时,f(x)=(x-1) ex,则f' (x)=xex,当x<0时,f' (x)<0,当x>0时,f' (x)>0,故f(x)的减区间为(-∞,0),增区间为(0,+∞).(2)设h(x)=xeax-ex+1,则h(0)=0,又h' (x)=(1+ax) eax-ex,设g(x)=(1+ax) eax-ex,则g' (x)=(2a+a2 x) eax-ex,若a>1/2,则g' (0)=2a-1>0,因为g' (x)为连续不间断函数,故存在x0∈(0,+∞),使得∀x∈(0,x0 ),总有g' (x)>0,故g(x)在(0,x0)为增函数,故g(x)>g(0)=0,故h(x)在(0,x0)为增函数,故h(x)>h(0)=-1,与题设矛盾.若0<a≤1/2,则h' (x)=(1+ax) eax-ex=e^(ax+ln(1+ax) )-ex,下证:对任意x>0,总有ln(1+x)<x成立,证明:设S(x)=ln(1+x)-x,故S' (x)=1/(1+x)-1=(-x)/(1+...
查看完整答案若正数a,b满足ab=a+b+3,则ab的取值范围是__________.
已知i,m,n是正整数,且1<i≤m<n.(Ⅰ)证明 niAim<miAin;(Ⅱ)证明 (1+m)n>(1+n)m.
已知α,β,γ是互不相同的锐角,则在sinαcosβ,sinβcosγ,sinγcosα三个值中,大于1/2的个数的最大值是【 】
已知 a > 0, b > 0, 且 a + b = 1, 则【 】
已知函数 f(x) = 2x − x − 1, 则不等式 f(x) > 0 的解集是【 】
已知 a > 0, b > 0, 且 ab = 1, 则 1/(2a)+1/(2b)+8/(a+b)的最小值为_______.
函数f(x)=|2x-1|-2lnx的最小值为__________.
设函数f(x)=a2x2+ax-3lnx+1,其中a>0.(1)讨论f(x)的单调性;(2)若y=f(x)的图像与x轴没有公共点,求a的取值范围.
设函数f(x)=ln(a-x),已知x=0是函数y=xf(x)的极值点.(1)求a;(2)设函数g(x)=(x+f(x))/(xf(x)).证明:g(x)<1.
已知函数f(x)=x3 - x2+ax+1.(1)讨论f(x)的单调性;(2)求曲线y=f(x)过坐标原点的切线与曲线y=f(x)的公共点的坐标.
设微分方程xdy-(y2-4y)dx=0(x>0),y(1)=2的解为y(x),函数y=y(x)的图像斜率恒不为0,则10y(√2)的值为________.
设函数f(x)=x-x³eax+b,曲线y=f(x)在点(1,f(1))的切线方程为y=-x+1.(1)求a,b的值;(2)设g(x)=f'(x),求g(x)的单调区间;(3)求f(x)极值点的个数.