在锐角三角形△ABC中,AB>AC,O为外心. 设D为BC上一点,O1,O2分别为△ABD,△ACD的外心,△AO1O2的外接圆与⨀O交于不同于A的点L.
证明:A,O,D三点共线当且仅当AL//BC.
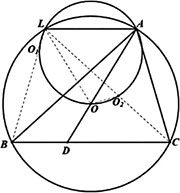
在锐角三角形△ABC中,AB>AC,O为外心. 设D为BC上一点,O1,O2分别为△ABD,△ACD的外心,△AO1O2的外接圆与⨀O交于不同于A的点L.
证明:A,O,D三点共线当且仅当AL//BC.

由萨蒙定理知A,O1,O,O2四点共圆.事实上,∠AO1 O=1/2∠AO1 B=∠ADC,同理可得∠AO2 O=∠ADB,∴∠AO1 O+∠AO2 O=180°.设BO1∩CO2=L,则∠ABO1=90°-∠ADC=∠ACO2,∴A,C,B,L四点共圆,即L在...
查看完整答案直角三角形之斜边上所画之正三角形之面积,等于其余两边上所画之正三角形之面积之和.
试证同底之三角形且在同平行线内其面积相等,又证明如何作一三角形令其面积等于已知之四边形.
设 D 为 △ABC 之底边 BC 之中点,若顶角 A 为角直角或锐角,则底边BC 分别大于,等于或小于中线 AD 之二倍.试证之.
设 ABC 为一直角三角形,A 为直角,A 之平分线与 BC 交于 D,与此三角形之外接圆交于 B.求证: △ABC 之面积 =1/2 AD×AE.
三角形ABC中,自A、B两点各作对边垂线,垂足为D、E,设M、N为DE及AB之两中点,证明MN⊥DE.
三角形ABC中,其边为a,b,c,内接圆半径为r,试证:a+b+c=2r(cot(A/2)+cot(B/2)+cot(C/2))
设P为平面凸多边形,若线段AB的两端点在P的边界上,并且过A,B与AB垂直的两条直线之间的区域(含边界)包含P,则称线段AB为“锦弦”. 求最大的正整数k,使得任意平面凸多边形P都有k条锦弦.
设ABCD为一平行四边形,AC为对角线,由B作任意直线各交AC、CD及AD于F、G及E,求证EF·FG=BF².
证从平行四边形之一顶点作线至对边之中点,三等分四边形之对角线.
AO 为圆之半径,过垂直于此之直径上一点 B,引任意弦 BP,从此弦之一端P 引切线 PC 与OB 之延线会于 C,证 CB =CP.
设二圆之连心线交一圆于 A,B 两点,交第二圆于 D,C 二点,又交二圆之一外公切线于 P 点,设在连心线上,点 A 距 P 最近,点 D 距 P 最远,试证:PA· PD = PB·PC.