高中数学-高考试题(全国统考 1962年圆)

计算题（1962年全国统考）

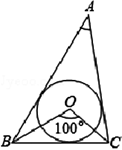
如图所示，O是△ABC的内心，∠BOC=100°，则∠BAC=______度.

答案解析

∵OB、OC是∠ABC、∠ACB的角平分线，∴∠OBC+∠OCB=180°-100°=80°，而∠OBC+∠OCB=1/2(∠ABC+∠ACB)=80°,∴∠ABC+∠ACB=160°∴∠BAC=18...

查看完整答案

讨论

高中数学

求sin⁡(2arcsin(⁡4/5))的值.

解方程lg(x-5)+lg(x+3)-2lg2=lg(2x-9).

求(1-2i)5的实部.

某工厂第三年产量比第一年增长21%,问平均每年比上一年增长百分之几?又第一年的产量是第三年的产量的百分之几?(精确到1%)

在2和30中间插入两个正数，这两个正数插入后使前三个数成等比数列，后三个数成等差数列，求插入的两个正数？

为了测湖岸边A、B两点的距离，选择一点C，测得CA=50米，CB=30米，∠ACB=120°，求AB.

证明：等腰三角形两腰上的高相等.

一条直线过点(1，-3)，并且与直线2x+y-5=0平行，求这条直线的方程.

一个正三棱柱形的零件，它的高是10cm，底面边长是2cm，求它的体积.

不查表求sin105°的值.

圆

从半圆之直径 AB 两端各引此半圆弦 AC,BD交于 E，求证: AC·AE+BD·BE = AB².

两圆外切，其半径各为R和r，设两圆之外公切线之交角为θ，试证 sinθ=.

A,B,C 为三定点，求作一圆过 A,B，使从 C 到此圆的切线等于定长.

已知PA,PB,PC为过圆周上点P三弦，PT为圆之切线，设有一直线与PT平行，交PA,PB,PC于A',B',C'三点.求证：PA∙PA'=PB∙PB'=PC∙PC'.

两圆面积比等于它们的半径比.

设 △ABC 是一个圆的内接三角形，过 A 作切线交于 BC 的延长线于 D.证明 △ABD,△ACD 的外接圆直径的比等于 AD:CD.

自 △ABC 的顶点 A 至对边作垂线，自垂足 D 作 AB、AC 过之垂线，其垂足为 E、F，证明 B,E,F,C 共圆.

设O为圆心，AB为弦，延长AB至C，令BC等于圆半径，再引CO交圆于D，求证：∠BOC为∠DOA的1/3.

于任意 △ABC 之各边上向外作等边三角形 BCD，CAE 及 ABF，试证此诸等边三角形的外接圆共点.若此点为 P，则 PA+PB + PC =AD =BE =CF.

如图，△ABC为给定的锐角三角形，其内切圆ω分别与边AB,AC切于点K,L.高AH分别与∠ABC,∠ACB的平分线交于点P,Q.设ω1,ω2分别为△KPB,△LQC的外接圆，AH的中点ω1,ω2外，求证：从AH的中点引向ω1,ω2的切线相等.

平面几何

试证三角形之高为垂足所成三角形之各角的角二等分线.

三角形内任意一点至三顶点 A,B,C 的延长线交对边于 P,Q,R，则BP/CP×CQ/AQ×AR/BR=1.

某城街路为棋盘式，走向南北者有 a 条，而走向东西者有 6 条，一行人欲由西北隅向最短之路走到东南隅，问计共有若干方法？

已知底边顶角及底边上之高,求作一三角形.

设 D 为 △ABC 之底边 BC 之中点，若顶角 A 为角直角或锐角，则底边BC 分别大于，等于或小于中线 AD 之二倍.试证之.

设 ABC 为一直角三角形，A 为直角，A 之平分线与 BC 交于 D，与此三角形之外接圆交于 B.求证: △ABC 之面积 =1/2 AD×AE.

对于已知圆，作一外接三角形，与已知三角形相似.

等积各三角形，证明其等腰者周界为极小，当其底相等时.

三角形ABC中，自A、B两点各作对边垂线，垂足为D、E，设M、N为DE及AB之两中点，证明MN⊥DE.

三角形ABC中，其边为a,b,c，内接圆半径为r，试证：a+b+c=2r(cot⁡(A/2)+cot(B/2)+cot(C/2))