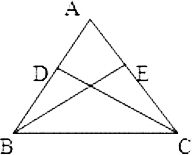
证明：等腰三角形两腰上的高相等.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
设 ABC 为一直角三角形，A 为直角，A 之平分线与 BC 交于 D，与此三角形之外接圆交于 B.求证: △ABC 之面积 =1/2 AD×AE.
三角形ABC中，自A、B两点各作对边垂线，垂足为D、E，设M、N为DE及AB之两中点，证明MN⊥DE.
三角形ABC中，其边为a,b,c，内接圆半径为r，试证：a+b+c=2r(cot(A/2)+cot(B/2)+cot(C/2))
在 △ABC 内作 AE 及 BD，假设 ∠CAE < ∠CBD，∠BAE < ∠ABD，求证 AE> BD.
△ABC 和△A'B'C'中，∠A >∠A’,则 BC >B'C'.
自 △ABC 的顶点 A 引 ∠B 的内外角平分线之垂线，则此两垂足与 AB，AC两边的中点共线.求证之.
如图，∠ABC=90°,AC=BC,AD⊥CE,BE⊥CE，垂足分别是D,E.已知AD=8,BE=3，则DE=______.