高中数学-高考试题(北京大学 1946年圆)

证明题（1946年北京大学；1946年清华大学；1946年南开大学）

两圆外切，其半径各为R和r，设两圆之外公切线之交角为θ，试证 sinθ=.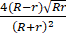

答案解析

暂无答案

讨论

高中数学

解下列联立三角方程式

从半圆之直径 AB 两端各引此半圆弦 AC,BD交于 E，求证: AC·AE+BD·BE = AB².

证明 △ABC 中过 B,C 二顶点之二中线等长，则 △ABC 为等腰，并证明其逆定理.

试证下列恒等式2 sec-1⁡x=tan-1⁡

解下列三角方程式：tanx+tan2x=tan3x.

求作一四角形，与一已知四角形等角而外切于一定圆.

试证: 直角三角形之弦上正方形之面积，与其他两边之平方形面积之和相等.

掷骰一粒，连掷十次，求掷得四次六点之几率.

已知log10⁡2=0.30103，试求下列对数之值

求与原点及直线x+4y=8等距离之点之轨迹方程式.

圆

作直线垂直于一已知线，与已知圆相切.

设G为半径为R的圆，G1,G2,⋯,Gn为半径为r的圆，已知G1,G2,⋯,Gn均外切于G，对于i=1,2,⋯,n-1，Gi与Gi+1外切，且Gn与G1外切，则下列叙述正确的有【】

已知直线 y = kx + b (k > 0) 与圆 x2 + y2 = 1 和圆 (x − 4)2 + y2 = 1 均相切, 则 k = _______, b = _______.

如图，AB是半圆的直径，C是半圆上一点，直线MN切半圆于C点，AM⊥MN于M点，BN⊥MN于N点，CD⊥AB于D点 . 求证：(1) CD=CM=CN；(2) CD2=AM•BN.

设 CEDF 是一个已知圆的内接矩形，过 D 作该圆的切线与 CE 的延长线相交于点 A ，与 CF 的延长线相交于点 B . 求证：BF/AE=BC3/AC3 .

半径为 1 , 2 , 3 的三个圆两两外切．证明：以这三个圆的圆心为顶点的三角形是直角三角形．

圆Γ的圆心为I.凸四边形ABCD满足：线段AB,BC,CD和DA都与Γ相切.设Ω是三角形AIC的外接圆. BA往A方向的延长线交Ω于点X,BC往C方向的延长线交Ω于点Z,AD往D方向的延长线交Ω于点Y,CD往D方向的延长线交Ω于点T.证明：AD+DT+TX+XA=CD+DY+YZ+ZC.

如图所示，O是△ABC的内心，∠BOC=100°，则∠BAC=______度.

沈括的《梦溪笔谈》是中国古代科技史上的杰作，其中收录了计算圆弧长度的“会圆术”.如图，(AB) ̂是以O为圆心，OA为半径的圆弧，C是AB的中点，D在(AB) ̂上，CD⊥AB.“会圆术”给出(AB) ̂的弧长的近似值s的计算公式：s=AB+CD2/OA.当OA=2,∠AOB=60°时，s=【】

过四点(0,0),(4,0),(-1,1),(4,2)中的三点的一个圆的方程为____________．

平面几何

Let n be a positive integer. A“Northern European Square Matrix (NESM) is an n×n square containing all the integers from 1 to n²,so that there is exactly one number in each grid.The two different grids are neighbours if they share a common edge.A grid is called a "valley”if the integer in it in smaller than the integers in all the neighbours of the grid. An "uphill path”is a sequence containing one or more grids satisfying:(i)the frist grid of the sequence is a valley,(ii) each subsequent grid in the sequence is the neighbour of its previous grid,(iii) the integers in the girds of the sequence is incremented.Figure out the minimum possible value of the number of uphill paths in a NESM which should be represented by a function of n.译文：令n为一个正整数，一个“北欧方阵”是一个包含1至n²所有整数的n×n的方格表，使得每个方格中恰有一个数字。两个相异方格如果有公共边，称它们是相邻的。如果一个方格内的数字比所有相邻方格内的数字都小，称其为“山谷”。一条“上坡路径”是一个包含一或多个方格的序列，满足：(1)序列的第一个方格是山谷；(2)序列中随后的每个方格都和前一个方格相邻；(3)序列中方格所写的数字递增。试求一个北欧方阵中山坡路径的最小可能值，以n的函数表示之。

三角形二边之和大于其他一边.

试证三角形之三中线相会于一点.

直角三角形之斜边上所画之正三角形之面积，等于其余两边上所画之正三角形之面积之和.

试证同底之三角形且在同平行线内其面积相等，又证明如何作一三角形令其面积等于已知之四边形.

试言已知三角形之两角及一角之对边,求作其形之方法.

如图，在三角形ABC中∠BAC=60°，BD平分∠ABC，交AC于D，CE平分∠ACB交AB于E，BD和CE交于F，则∠EFB=【】

设 AD 为 ∠ABC 之中线；∠ADB 之平分线交 AB 于E，∠ADC 之平分线交AC 于F，试证 EF// BC.

给定整数n > 1 ．在一座山上有n2个高度互不相同的缆车车站．有两家缆车公司 A 和B，各运营 k 辆缆车；每辆从一个车站运行到某个更高的车站（中间不停留其他车站） . A 公司的 k 辆缆车的k个起点互不相同， k 个终点也互不相同，并且起点较高的缆车，它的终点也较高． B 公司的缆车也满足相同的条件．我们称两个车站被某家公司连接，如果可以从其中较低的车站通过该公司的一辆或多辆缆车到达较高的车站（中间不允许在车站之间有其他移动）. 确定最小的正整数 k ，使得一定有两个车站被两家公司同时连接．(印度供题）

Consider the convex quadrilateral ABCD. The point P is in the interior of ABCD. The following ratio equalities hod:∠PAD:∠PBA:∠DPA=1:2:3=∠CBP:∠BAP:∠BPC.Prove that the following three lines meet in a point : the internal bisectors of angles ∠ADP and ∠PCB and the perpendicular bisector of segment AB.设P是凸四边形ABCD内部一点，且满足：∠PAD:∠PBA:∠DPA=1:2:3=∠CBP:∠BAP:∠BPC.证明：∠ADP的内角平分线、∠PCB的内角平分线和线段AB的中垂线，三线共点。（波兰供题）