高中数学-高考试题(全国统考 1978年圆)

证明题（1978年全国统考）

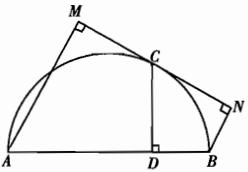
如图，AB是半圆的直径，C是半圆上一点，直线MN切半圆于C点，AM⊥MN于M点，BN⊥MN于N点，CD⊥AB于D点 . 求证：

(1) CD=CM=CN；

(2) CD²=AM•BN.

答案解析

(1) 连接CA、CB，则∠ACB=90° ∠ACM=∠ABC (弦切角等于同弧所对的圆周角)∠ACD=∠ABC (同角的余角相等)∴∠ACM=∠ACD.∴∆ACM≅∆ADC.∴CM=CD.同理 CN...

查看完整答案

讨论

高中数学

已知方程 kx2+y2=4 ，其中k为实数。对于不同范围的k值，分别指出方程所代表图形的类型，并画出显示其数量特征的草图．

全国统考幂函数

不查表，求 cos80°cos35°＋ cos10°cos55°的值．

求函数y=的定义域.

已知正方形的边长为 a ，求侧面积等于这个正方形的面积、高等于这个正方形边长的直圆柱体的体积

分解因式：x2-4xy+4y2-4z2.

证明：存在正常数c具有卜述性质：对任意整数n>1，以及平面上n个点的集合 S ，若 S中任意两点之间的距离不小于 1 ，则存在一条分离 S 的直线l , 使得 S 中的每个点到直线的距离不小于cn-1/3 . （我们称直线l分离点集 S , 如果某条以S中两点为端点的线段与l相交．)注．如果证明了比cn-1/3 弱的估计cn-α ，会根据α>1/3 的值，适当给分．(中国台湾供题)

有一叠n>1 张卡片．在每张卡片上写有一个正整数．这叠卡片具有如下性质：其中任意两张上的数的算术平均值也等于这叠卡片中某一张或几张卡片上的数的几何平均值．确定所有的n，使得可以推出所有卡片上的数均相等．(爱沙尼亚供题)

给定整数n > 1 ．在一座山上有n2个高度互不相同的缆车车站．有两家缆车公司 A 和B，各运营 k 辆缆车；每辆从一个车站运行到某个更高的车站（中间不停留其他车站） . A 公司的 k 辆缆车的k个起点互不相同， k 个终点也互不相同，并且起点较高的缆车，它的终点也较高． B 公司的缆车也满足相同的条件．我们称两个车站被某家公司连接，如果可以从其中较低的车站通过该公司的一辆或多辆缆车到达较高的车站（中间不允许在车站之间有其他移动）. 确定最小的正整数 k ，使得一定有两个车站被两家公司同时连接．(印度供题）

There are 4n pebbles of weights 1,2,3,…,4n. Each pebble is coloured in one of n colours and there are four pebbles of each colour. Show that we can arrange the pebbles into two piles so that the following two conditions are both satisfied:● The total weights of both piles are the same.● Each pile contains two pebbles of each colour.有 4n 枚石子，重量分别为 1 , 2 , 3 , … ， 4n ．每一枚小石子都染了n种颜色之一，使得每种颜色的小石子恰有四枚．证明：可以把这些小石子分成两堆，且满足以下两个条件：● 两堆小石子的总重量相同；● 每堆中每种颜色的小石子各有两枚．(匈牙利供题)

圆

已知PA,PB,PC为过圆周上点P三弦，PT为圆之切线，设有一直线与PT平行，交PA,PB,PC于A',B',C'三点.求证：PA∙PA'=PB∙PB'=PC∙PC'.

两圆面积比等于它们的半径比.

设 △ABC 是一个圆的内接三角形，过 A 作切线交于 BC 的延长线于 D.证明 △ABD,△ACD 的外接圆直径的比等于 AD:CD.

自 △ABC 的顶点 A 至对边作垂线，自垂足 D 作 AB、AC 过之垂线，其垂足为 E、F，证明 B,E,F,C 共圆.

设O为圆心，AB为弦，延长AB至C，令BC等于圆半径，再引CO交圆于D，求证：∠BOC为∠DOA的1/3.

于任意 △ABC 之各边上向外作等边三角形 BCD，CAE 及 ABF，试证此诸等边三角形的外接圆共点.若此点为 P，则 PA+PB + PC =AD =BE =CF.

如图，△ABC为给定的锐角三角形，其内切圆ω分别与边AB,AC切于点K,L.高AH分别与∠ABC,∠ACB的平分线交于点P,Q.设ω1,ω2分别为△KPB,△LQC的外接圆，AH的中点ω1,ω2外，求证：从AH的中点引向ω1,ω2的切线相等.

如图所示，在△BC中，M是边AC的中点，D,E是△ABC的外接圆在点A处的切线上的两点，满足MD//AB，且A是线段DE的中点，过A,B,E三点的圆与边AC相交于另一点P，过A,D,P三点的圆与DM的延长线相交于点Q.证明：∠BCQ=∠BAC.

Let ABC be an acute-angled triangle with AB > AC. Let P be the intersection of the tangents to the circumcircle of ABC at B and C. The line through the midpoints of line segments PB and PC meets lines AB and AC at X and Y respectively.Prove that the quadrilateral AXPY is cyclic.【译】在锐角三角形ABC中，AB>AC，△ABC的外接圆在点B和点C处的切线交于点P.一条同时过PB和PC中点的直线与AB,AC分别交于点X,Y.求证：A,X,P,Y四点共圆.

Let BC be a fixed segment in the plane, and let A be a variable point in the plane not on the line BC. Distinct points X and Y are chosen on the rays (CA) ⃗ and (BA) ⃗, respectively, such that ∠CBX=∠YCB=∠BAC.Assume that the tangents to the circumcircle of ABC at B and C meet line XY at P and Q, respectively, such that the points X,P,Y, and Q are pairwise distinct and lie on the same side of BC. Let Ω1 be the circle through X and Y centred on BC. Similarly let Ω2 be the circle through Y and Q centred on BC. Prove that Ω1 and Ω2 intersect at two fixed points as A varies.【译】在同一平面内，BC为给定线段，动点A不在直线BC上. X和Y分别为射线(CA) ⃗，射线(BA) ⃗上不重合的两点，满足∠CBX=∠YCB=∠BAC.若三角形ABC外接圆在点B和C处的切线分别交直线XY于点P和点Q，点X,P,Y,Q不重合，且位于直线BC同侧.圆Ω1经过点X,P且圆心在BC上.类地，圆Ω2经过点Y,Q且圆心在BC上.证明：当点A运动时，圆Ω1和圆Ω2始终交于两定点.

平面几何

设n是一个正整数.日式三角是将1+2+…+n个圆排成正三角形的形状,使得对 i= 1,2，…,n,从上到下的第i行恰有个圆，且其中恰有一个被染为红色.在日式三角内，忍者路径是指一串由n个圆组成的序列，从最上面一行的圆开始，每次从当前圆连接到它下方相邻的两个圆之一，直至到达最下面一行的某个圆为止.下图为一个n=6的日式三角,其中画有一条包含两个红色圆的忍者路径.求最大的整数k(用n表示),使得在每个日式三角中都存在一条忍者路径,它包含至少k个红色圆.

已知直线 y = kx + b (k > 0) 与圆 x2 + y2 = 1 和圆 (x − 4)2 + y2 = 1 均相切, 则 k = _______, b = _______.

沈括的《梦溪笔谈》是中国古代科技史上的杰作，其中收录了计算圆弧长度的“会圆术”.如图，(AB) ̂是以O为圆心，OA为半径的圆弧，C是AB的中点，D在(AB) ̂上，CD⊥AB.“会圆术”给出(AB) ̂的弧长的近似值s的计算公式：s=AB+CD2/OA.当OA=2,∠AOB=60°时，s=【】

过四点(0,0),(4,0),(-1,1),(4,2)中的三点的一个圆的方程为____________．

任意之外切四边形，相对两边之和等于其他相对两边之和，试证明之.

If two circles tangent at C and a common exterior tangent touches the circles in A and B, the angle ACB is a right angle.

内接于圆之平行四边形为矩形，其对角线通过圆心，试证明之.

求内接于圆之正六角形与外切正三角形之面积之比.

两圆相外切 (tangent externally) 于 A，又有一外公切线 (common external tangent) 切两圆于 B 及 C，试证 ∠BAC 为直角(right angle).

已知三角形之三角及其面积，求作其圆.