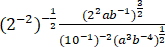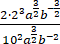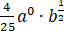高中数学-高考试题(全国统考 1978年幂函数)

计算题（1978年全国统考）

化简：

答案解析

原式=

=

=

=

=

讨论

基本初等函数

将函数f(x)=ex展开为x的幂级数，并求出收敛区间.( e=2.718为自然对数)

计算：30+3-1 -()1/2.

已知2a=5,⁡log83=b，则4a-3b=【】

求4x+49y-28之平方根.

试求 (根号内至无穷)

∛17与∜21之两数孰大________.

方程=5-16的所有正实数解的乘积为________.

管理综合指数函数

求a³/b及b³/a之正等比中项.

北京大学指数函数

幂函数

Evaluate to four significant figure by logarithm,

已知a>0且a≠1，函数f(x)=xa/ax (x>0).(1)当a=2时，求f(x)的单调区间；(2)若曲线y=f(x)与直线y=1有且仅有两个交点，求a的取值范围.

化简下式：(1 - c2)-1/2 - {[(1+c)(1-c)]1/2+c2[(1+c)(1-c)]-1/2}.

圣约翰大学幂函数

解不等式<2logax - 1(a>0,a≠1).

设复数z=3cosθ+i∙sinθ.求函数y=θ-argz(0<θ<π/2)的最大值以及对应的θ值.

设{an}是公比为q的等比数列，Sn是它的前n项和.若{Sn}是等差数列，则q=________.

已知复数z的模为2,则|z-i|的最大值为【】

在50件产品中有4件是次品，从中任意抽出5件，至少有3件是次品的抽法共________种(用数字作答)。

建造一个容积为8m3，深为2m的长方体无盖水池。如果池底和池壁的造价每平方米分别为120元和80元，那么水池的最低总造价为________元。

函数

已知函数f(x)的定义域为[0,+∞)，且满足f(x)=f(1/(1+x))，记函数的值域为Af，若a>0，满足{y│y=f(x),x∈[0,a] }=Af，则实数a的取值范围为__________.

Let R+ denote the set of positive real numbers. Find all functions f:R⟶R such that for each x∈R+, there is exactly one y∈R+ satisfying：xf(y)+yf(x)≤2.译文：设R+表示所有正实数构成的集合.求所有函数f:R+→R+，使得对任意x∈R+，恰好有一个y∈R+满足条件：xf(y)+yf(x)≤2.

设函数f(x)=，若f(x0)>1，则x0的取值范围是【】

定义函数f(x)代表|x|-2与x2-ax+3a-5中较小的数.若f(x)至少有3个零点，则a的取值范围为__________.

若xi为大于1的整数，记f(xi)为xi的最大素因数.令xi+1=xi-f(xi)（i为自然数）.(1)证明：对任意大于1的整数x0，存在自然数k(x0)，使得xk(x0)+1=0;(2)令V(x0)为f(x0 ),f(x1 ),⋯,f(xk(x0))中不同的个数，求V(2),V(3),⋯,V(781)中的最大数，并说明理由.

某日温度华氏与摄氏之比若 13:4，问华氏几度?

220之竞走，甲许乙先发5码，乙许丙先发9码，则无胜负；若于880码竞走，问甲许丙先发 50 码，尚胜若干码?

有甲、乙两人，甲所有银为乙之五倍，其后甲得30元，乙得80元，则甲所有为乙之二倍，问甲、乙原各有银几何?

由甲地至乙地，若每时行 32 丈，则比预定时间迟2小时可到，若每小时行 56 丈，则比预定时间早1小时可到，问依预定时间每时应行之速?

北京工业大学映射与函数