高中数学-高考试题(全国统考 1999年基本不等式)

计算题（1999年全国统考）

解不等式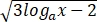<2log_ax - 1(a>0,a≠1).

答案解析

原不等式等价于由①得loga⁡x≥2/3，由②得loga⁡x<3/4,或loga⁡x>1，由③得loga⁡x>1/2.由此得2/3≤loga⁡x<3/4, 或loga⁡x>1当a>1时得所...

查看完整答案

讨论

基本不等式

已知 a > 0, b > 0, 且 ab = 1, 则 1/(2a)+1/(2b)+8/(a+b)的最小值为_______.

不等式(2-x)/(x+4)>0的解集是__________.

已知 a, b ∈ R, 则下列各式正确的是【】

当sin2x>0时，求不等式log0.5(x2-2x-15)>log0.5(x+13)的解集.

已知n为自然数，实数a>1，解关于x的不等式logax - 4loga2x + 12loga3x + ⋯ + n(-2)n-1loganx > (1-(-2)n)/3·loga(x2 - a).

对任意x，y，x2+y2-xy=1，则【】

若实数a,b满足a>b>0，下列不等式中恒成立的是【】

解不等式>x+a,(a>0)并就图说明之.

正实数x,y,z,w满足x≥y≥w，且x+y≤2(w+z)，求 + 的最小值.

已知 a > 0, b > 0, 且 a + b = 1, 则【】

对数函数

设a>0,a≠1,t>0，比较1/2logat与loga (t+1)/2的大小，并证明你的结论.

已知a>0,a≠1，试求使方程loga(x-ak)=(x2-a2)有解的k的取值范围.

已知log5(x2+2x-2) = 0 , 2log5(x+2) - log5y + 1/2 = 0，求y的值.

log89/log23 的值是【】

若loga2<logb2<0，则【】

已知y=loga(2-ax)在[0,1]上是x的减函数,则a的取值范围是【】

求(lg3+lg2)/(1/4 lg16++1/2 lg0.09)的值.(其中lg表示以10为底的对数)

设logx⁡(2x2+x-1)>logx⁡2-1，则x的取值范围为【】.

若f(x)=ln⁡|a+1/(1-x)|+b是奇函数，则a=_____，b=______．

计算(2log4⁡3+log8⁡3)(log3⁡2+log9⁡2)的值为【】

不等式

设 a, b, c ∈ R, a + b + c = 0, abc = 1.(1) 证明: ab + bc + ca < 0;(2) 用 max{a, b, c} 表示 a, b, c 的最大值, 证明: max{a, b, c} ⩾.

The real numbers a,b,c,d are such that a≥b≥c≥d>0 and a+b+c+d=1.Prove that (a+2b+3c+4d)aabbccdd<1.设实数a、b、c、d满足 a≥b≥c≥d>0 ，且 a+b+c+d=1 . 证明：(a+2b+3c+4d)aabbccdd<1.(比利时供题)

设a,b是满足ab<0的实数，那么【】

不等式|x2-3x|>4的解集是____________.

不等式 < 1的解集是__________.

湖南省二元一次不等式组

已知a,b,c是实数，函数f(x)=ax2+bx+c,g(x)=ax+b，当-1≤x≤1时，|f(x)|≤1.（Ⅰ）证明：|c|≤1；（Ⅱ）证明：当-1≤x≤1时，|g(x)|≤2;（Ⅲ）设a>0，当-1≤x≤1时，g(x)的最大值为2，求f(x).

不等式组的解集是【】

设a²+b²+c²=1,x²+y²+z²=1，证ax+by+cz≤1.

若 x, y 满足约束条件则 z = x + 7y 的最大值为 __________.